O Processo de Energização de uma Linha de Transmissão – Parte 1

Neste post será analisado, inicialmente de forma simplificada, o que ocorre quando uma linha é energizada, desde o seu terminal emissor até o seu terminal receptor. Neste primeiro contato com o tema, para contextualizar os fenômenos presentes, a linha será considerada ideal, ou seja, sem perdas (sem elemento resistivo série ou condutivo em paralelo).

Nesta modelagem simplificada, a linha pode ser representada conforme circuito unifilar apresentado na Figura 1, na qual encontram-se presentes: uma fonte em corrente contínua (“U”), a chave que será fechada no instante “t=0”, o terminal emissor com tensão representada por “U₁ “, as indutâncias série “l” e as capacitâncias paralelas “c”, presentes em cada segmento elementar de linha, “delta x”, e o terminal receptor, submetido à tensão “U₂“. A linha possui um comprimento total “L” km.

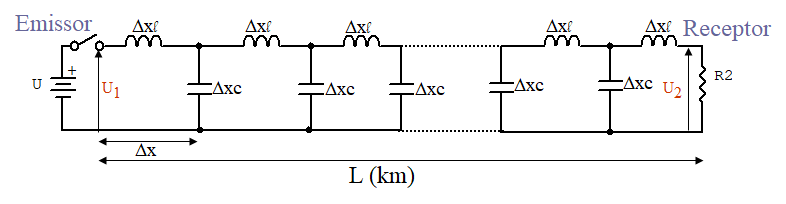
Após decorrido um intervalo de tempo “delta t” do fechamento da chave, o gráfico do perfil da tensão ao longo da linha encontra-se representado na Figura 2. Neste gráfico, para o período de tempo analisado, observa-se que seria energização, apenas, o primeiro segmento elementar de linha “delta x”. Tal energização fica caracterizada pelo surgimento de uma tensão “U” no primeiro capacitor “delta x . c” e a passagem de uma corrente “I” no primeiro indutor “delta x . l”

Este mesmo gráfico, decorridos dois intervalos de tempo “delta t”, teria a forma apresentada na Figura 3, na qual se observa que dois segmentos elementares estariam energizados. Nesta figura se infere, também, que o processo de energização terá uma velocidade dada por:

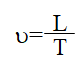
onde T representa o tempo para que a tensão no receptor, U₂, venha ser submetida ao valor “U”.

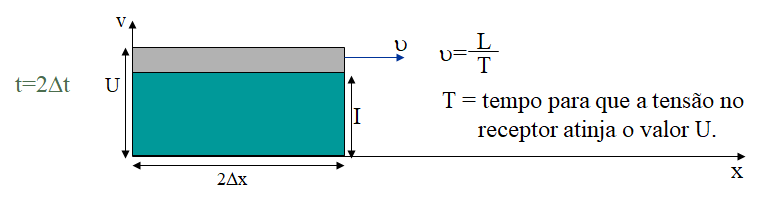
Ao analisar esse processo de energização, quando um trecho de 1 km de linha já estiver energizado, conforme ilustração contida na Figura 3, as seguintes constatações poderiam ser verificadas:

• carga elétrica acumulada no trecho: q=Uc [Coulomb];
• corrente através da seção do condutor: I₀=qv=Ucv [A];
• impedância de entrada da linha:

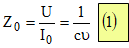
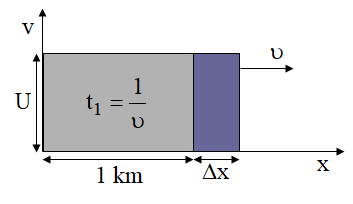
Retomando a energização de um segmento elementar “delta x”, poderiam ser feitas, também, as seguintes considerações:

• “delta t” = período para que a corrente cresça de 0 até I_o [A];
• nesta ocasião surgiria a seguinte força contra eletromotriz induzida:

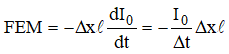
• o intervalo de tempo “delta t” e a força contra eletromotriz induzida poderiam ser escritos da seguinte forma:

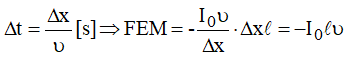
• essa força contra eletromotriz deve ser neutralizada pela fonte para que a corrente I₀ possa fluir, portanto:

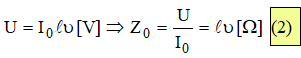
Igualando (1) e (2), obtém-se a expressão para cálculo da velocidade com a qual o processo de propagação decorre:

Para linhas aéreas, essa velocidade é muito próxima da velocidade da luz no vácuo.

Por outro lado, a partir da equação (2), substituindo a expressão da velocidade obtida, se chegaria a:

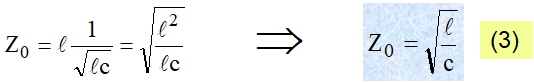
Para linha a dois condutores, no ar, por exemplo, desprezando o efeito do fluxo magnético interno no condutor e da presença do solo:

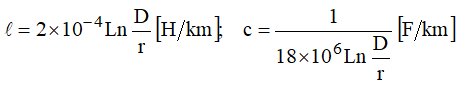
Substituindo essas equações em (3):

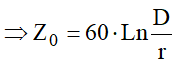
Portanto Z₀ não depende do comprimento da linha, somente do meio em que esta se encontra e de suas dimensões físicas. Z₀ recebe o nome de “Impedância Natural da Linha”.

Uma outra grandeza importante, neste processo de energização, é a corrente de carga da linha:

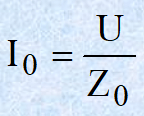
As seguintes observações podem ser feitas sobre esta corrente:

• a corrente de carga da linha, excitada por uma fonte de tensão constante, também independe do seu comprimento;
• esta constatação está associada ao fato de que a corrente de carga, quando começa a fluir, desconhece o comprimento da linha e a forma pela qual ela é terminada; esta consideração representa uma “ruptura de paradigmas” em relação a circuitos simples, até aqui analisados; esses circuitos se caracterizavam por “parâmetros concentrados”, ou seja, os valores das indutâncias e capacitâncias eram concentrados no espaço; por outro lado, o circuito da linha de transmissão se caracteriza por “parâmetros distribuídos” ao longo do espaço; ou seja, os fenômenos que vão surgir dependem do comprimento da linha, algo que não se leva em consideração em circuitos a parâmetros concentrados.

Uma outra visão atrelada ao processo de energização está associada com as relações de energia em jogo:

• em cada intervalo de tempo “delta t”, necessário para energizar um trecho de comprimento “delta x” de linha, a fonte fornece à mesma uma quantidade de energia igual a UI₀ vezes “delta t”;
• esta energia fornecida será armazenada em dois campos, no magnético:

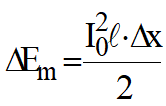
• no elétrico:

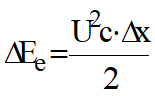
O armazenamento se dá simultaneamente, de tal forma que:

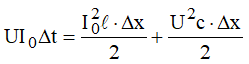
Substituindo:

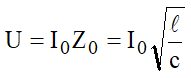
em:

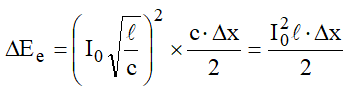
Observa-se, portanto, que a quantidade de energia armazenada no campo elétrico é exatamente igual à quantidade de energia armazenada no campo magnético.

Uma outra análise está associada ao que ocorre, quando o processo de energização chega ao terminal receptor, caracterizado na Figura 4 como terminal 2, conectado a uma impedância Z₂.

Neste caso, três considerações precisam ser feitas:

• Z₂>Z₀ a corrente que irá circular por Z₂ terá que ser reduzida, caracterizando um excesso de energia no campo magnético; como se trata de uma linha ideal, não há dissipação de energia, o excesso será transferido para o campo elétrico, elevando a tensão no terminal, conforme ilustração contida na Figura 5, observando-se, inclusive, que tal balanço de energia irá repercutir ao longo do perfil de toda a linha;

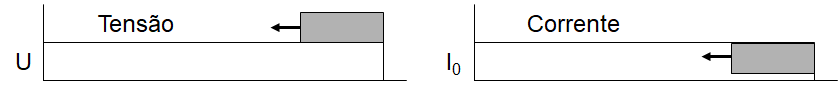
• Z₂<Z₀ neste caso, a corrente que irá circular por Z₂ terá que ser aumentada, ou seja, existe deficit de energia no campo magnético que será suprido pelo campo elétrico; o perfil de tensão e corrente terá um comportamento “dual” em relação ao caso anterior, conforme ilustração registrada na Figura 6;

• Z₂=Z₀ esta é uma situação em que não ocorrerá desequilíbrio energético no terminal 2; toda a energia magnética será perfeitamente absorvida pela impedância e os perfis de tensão e corrente ao longo da linha não sofrerão alteração.

Dois casos particulares podem ser analisados: o terminal receptor encontra-se aberto, e, no segundo caso, o mesmo terminal encontra-se em curto-circuito.

No primeiro caso, a corrente no terminal terá que ser reduzida a zero; como consequência o campo elétrico terá que armazenar toda a energia emitida pela fonte. A Na Figura 7, essa situação encontra-se ilustrada.

Neste caso, a energia, em função da tensão terminal U₂ , seria dada pela expressão:

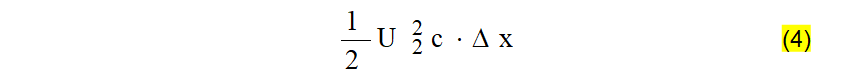
Por outro lado, a energia que a linha já possuía, pode ser obtida por:

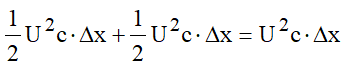
Em mais um intervalo de tempo “delta t” a fonte envia mais uma quantidade de energia dada por U²c.delta x. A energia a ser armazenada no campo elétrico será, portanto:

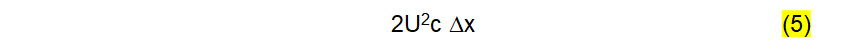
Uma vez que as equações (4) e (5) traduzem o mesmo fenômeno de armazenamento da energia, no último trecho “delat x” da linha, elas têm que ser numericamente iguais, portanto:

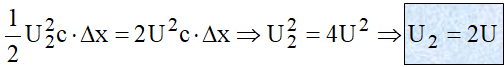
Ou seja, A tensão no terminal receptor cresce ao dobro da tensão aplicada no terminal emissor.

Situação dual ocorreria, caso o terminal receptor se encontrasse em curto-circuito, caracterizando que a corrente I₂ atingiria o valor de 2I₀.

O conceito de Ondas Viajantes

Esse é um conceito herdado da Engenharia Hidráulica, adaptado para explicar o processo de energização de uma linha de transmissão. Ao se fechar a chave ilustrada na Figura 1, partem simultaneamente duas ondas viajantes U [V] e I₀ [A], com velocidade de propagação v [m/s].

A depender da terminação, podem surgir ondas refletidas que viajam na mesma velocidade de propagação v [m/s]. Em qualquer ponto ao longo da linha a tensão e corrente passam a ser dadas por:

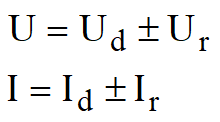
onde U_d e I_d representam as ondas de tensão e de corrente, respectivamente, que viajam no sentido direto (da esquerda para a direita), e U_r e I_r são as ondas de tensão e de corrente, respectivamente, que viajam no sentido reverso (da direita para a esquerda).

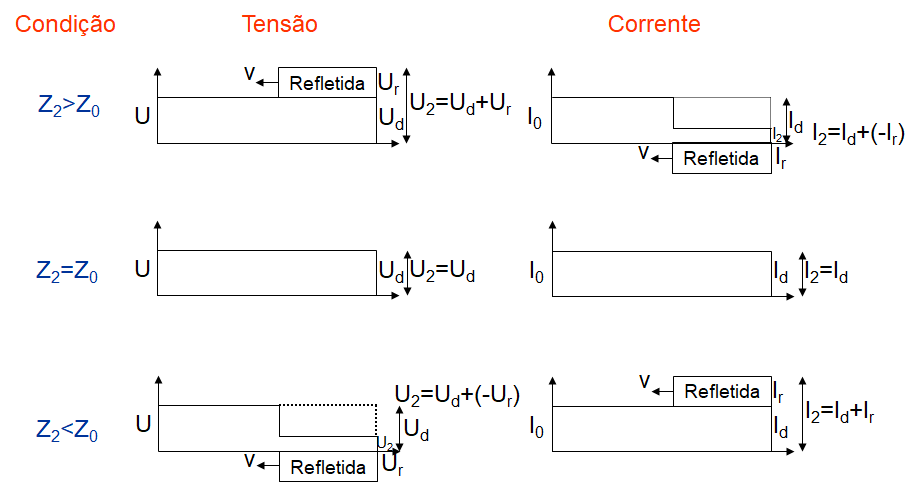
Quando do encontro das terminações, ilustradas na Figura 4, as três considerações feitas anteriormente tomam os formatos ilustrados na Figura 8, na qual as ondas viajantes refletidas passam a possuir sinal positivo ou negativo a depender da relação entre Z₂ e Z₀. As ondas refletidas passam a se sobrepor às ondas incidentes, aumentando ou diminuindo as grandezas de tensão ou corrente, readequando o perfil desses valores ao longo da linha de transmissão. A condição Z₂=Z₀ é caracterizada como uma situação em que não surgirão ondas refletidas.

Coeficientes de Reflexão

Uma análise importante está relacionada à ideia de se inferir os valores das tensões e correntes refletidas em função das grandezas incidentes e das impedâncias presentes. Das análises anteriores, é possível escrever:

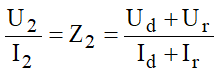
Como:

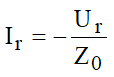
e:

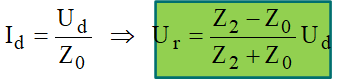
Da mesma forma, colocando:

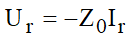
e:

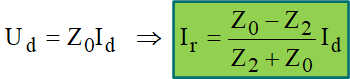
Portanto, são definidos o coeficiente de reflexão das tensões:

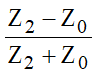
e das correntes:

Home

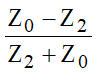
Diagrama de Treliças

O diagrama de treliças desempenha um papel acadêmico muito importante para se visualizar como as ondas viajantes se desenvolvem ao longo do tempo e do espaço. Permite, também, construir o comportamento da tensão em pontos específicos da linha de transmissão, como, por exemplo, os seus terminais. Na Figura 9 são ilustradas uma linha de transmissão, sendo energizada a partir de uma fonte, com impedância interna Z₁ e o diagrama de treliças associado. Neste diagrama, o eixo horizontal representa o deslocamento da onda viajante ao longo da linha e o eixo vertical permite aferir o seu desenvolvimento ao longo do tempo. O tempo “T” representa a duração da onda percorrer toda a linha de transmissão, desde o terminal emissor até o terminal receptor. Os coeficientes de reflexão estão identificados como K₁ para o terminal emissor e K₂ para o terminal receptor. “L” representa a extensão da linha.

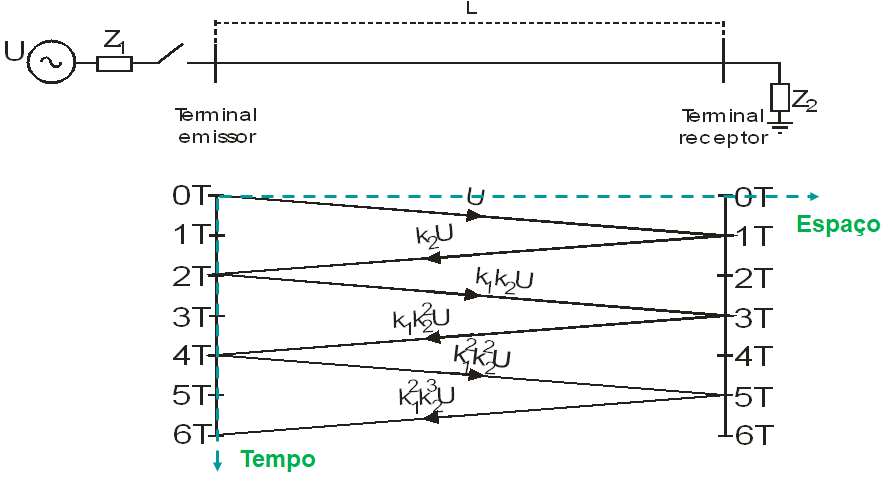
Na Tabela 1, encontram-se registrados todos os valores das tensões nos dois terminais, escolhendo-se criteriosamente os intervalos de tempo de interesse, os quais são caracterizados por momentos anteriores a chegada de cada onda viajante no terminal observado. É importante lembrar que, quando do impacto da onda viajante em cada terminal, ocorrerá um acréscimo de tensão no terminal, caracterizado pela soma algébrica da tensão incidente mais a tensão refletida.

A título de exemplo numérico, a Tabela 1 encontra-se convertida na Tabela 2, a qual retrata a condição de uma fonte de corrente contínua ideal (Z₁=0), com valor de 1 pu e o terminal receptor aberto.

Os gráficos das tensões nos dois terminais encontram-se ilustrados na Figura 10. O gráfico referente ao terminal emissor caracteriza um resultado plenamente esperado, uma vez que ele está alimentado por uma fonte ideal, a qual impõe o valor da tensão (igual a 1 pu, para o caso). Já o gráfico referente ao terminal receptor caracteriza uma situação bastante inusitada: enquanto a fonte de tensão emite um sinal constante de 1 pu, este sinal será alternado, variando entre 0 e 2 pu, incorporando uma sobretensão significativa a este terminal.

Exemplos com o Uso do Aplicativo ATP

A viabilidade acadêmica das ondas viajantes pôde ser vista através do diagrama de treliças para situações simples. Na prática, entretanto, surgem casos mais complexos, os quais requerem o suporte de aplicativos computacionais. O exemplo anterior será repetido com o uso do ATP, assim como serão enfocadas outras situações que envolvem condições mais reais.

Serão analisados os 5 casos ilustrados nos circuitos mostrados na Tabela 1. Cada circuito simula uma das seguintes situações [3]:

1. caso ideal, com fonte constante sem perdas e linha de transmissão sem perdas;
2. idem caso 1, incluindo as perdas da linha de transmissão;
3. idem caso 2, porém com fonte senoidal;
4. idem caso 3, porém acrescentando-se uma indutância em série com a fonte;
5. idem caso 4, porém sendo a linha de transmissão trifásica.

Na Tabela 3 são registrados os circuitos montados no ATP para cada um dos casos analisados. Observe que, em todos os casos, está havendo monitoração da tensão nos dois terminais.

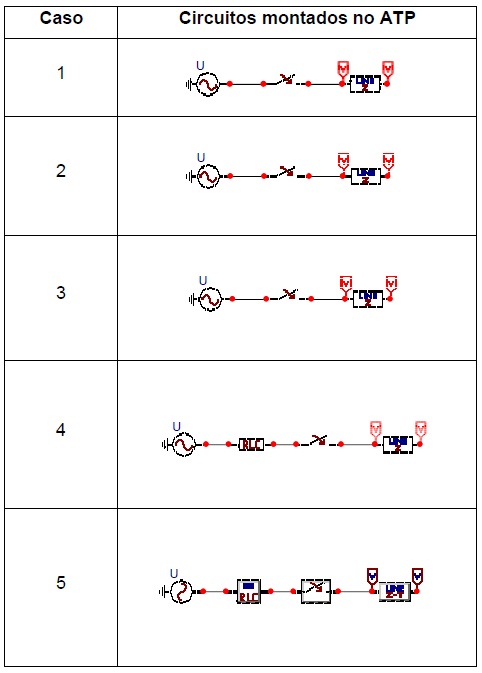
Os elementos dos circuitos analisados e as configurações de simulação encontram-se registados nas Tabelas 4 a 15.

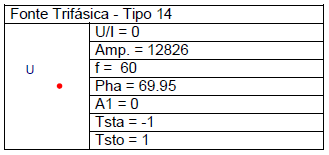
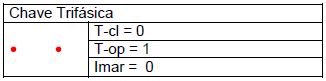
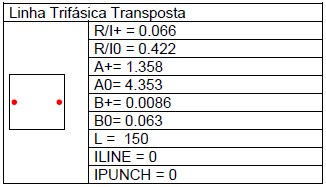
O primeiro caso é o mesmo já resolvido através do diagrama de treliças. Na Figura 11 é apresentado o resultado gráfico obtido, o qual reproduz a situação já ilustrada na Figura 10.

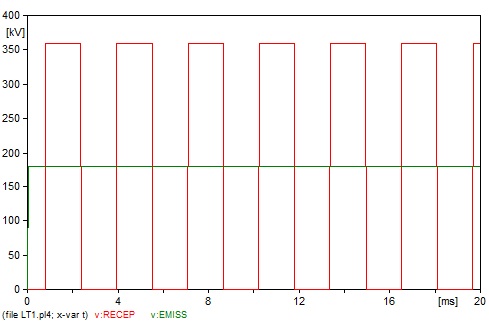
Os demais resultados encontram-se registrados nas Figuras 12 a 15.

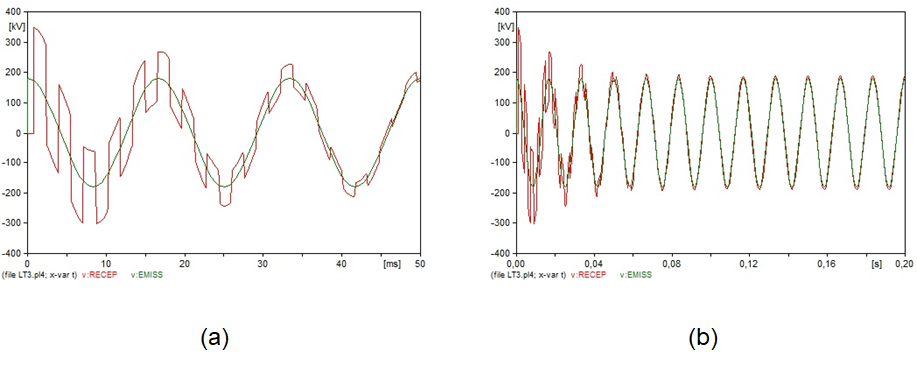
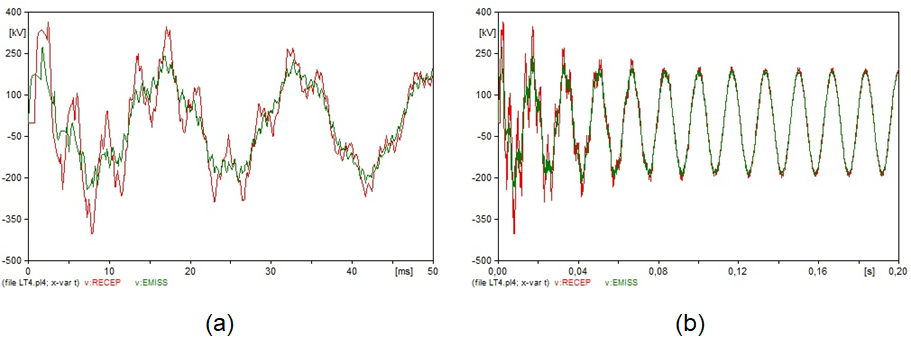
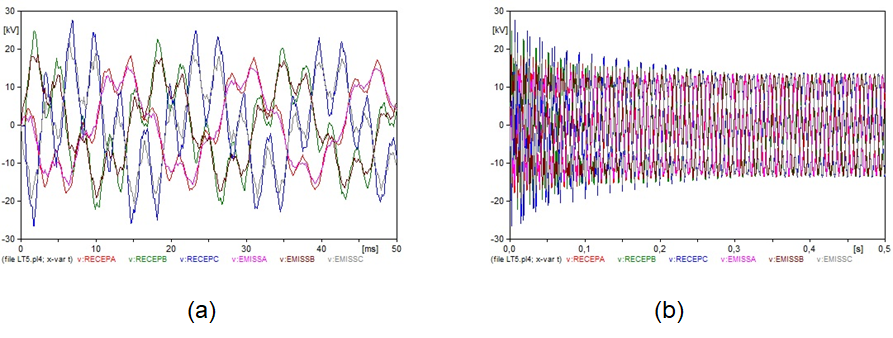
Observa-se que, em todos os casos simulados, os quais incorporaram a presença de elementos resistivos (circuitos 2, 3, 4 e 5), houve uma amortização da sobretensão no terminal receptor, caracterizada pela dissipação do excesso de energia, através do efeito Joule. Apenas no circuito 1, o qual representa uma situação de uma linha ideal, sem elementos resistivos, o excesso de energia continuaria circulando no circuito e o terminal receptor ficaria indefinidamente submetido às sobretensões. Uma outra observação para esses circuitos (2, 3, 4 e 5) é que os valores da tensão no terminal receptor convergem para os valores impostos pela fonte de tensão, após a amortização.

Sobre os casos analisados, ficam os seguintes pontos para reflexão:

• quais seriam os impactos nos gráficos apresentados nas Figuras 11, 12, 13, 14 e 15 se, em vez de 150 km, a linha tivesse uma extensão de 75 km?
• sobre essas mesmas figuras, o que ocorreria se a chave fosse fechada, quando a fonte estivesse passando por um momento angular diferente?

Home

CONSIDERAÇÕES FINAIS

Neste post foram introduzidos diversos conceitos associados à energização de uma linha de transmissão. Inicialmente, para simplificar os modelos, foi considerada uma linha ideal, sobre a qual os conceitos foram paulatinamente concebidos. Duas ferramentas importantes auxiliaram na avaliação dos diversos fenômenos envolvidos na energização de uma linha: o diagrama de treliças e o aplicativo ATP. Com o apoio dessa última ferramenta foi possível analisar casos mais complexos, próximos de situações mais reais. No próximo post, essas análises serão retomadas em linhas reais, alimentadas por fontes senoidais, sobre as quais serão aplicados, rigorosamente, tratamentos matemáticos que permitam exprimir os fenômenos físicos envolvidos.

REFERÊNCIAS BIBLIOGRÁFICAS

[1] Fuchs, Rubens Dario -Transmissão de Energia Elétrica, Livros Técnicos e Científicos S. A. Editora EDUFU UNIVERSIDADE FEDERAL DE UBERLÂNDIA. 2015.

[2] H. W. Dommel and S. Meyer, Eletromagnetic Transients Program (EMTP)/Alternative Transient Program (ATP). Version 2019. Bonneville Power Administration, Portland, OR, USA: BPA and Leuven EMTP Centre (LEC), 1960_2019.

[3] Bezerra, J. M. B. e Nepomuceno, F. Disciplina Equipamentos Elétricos – Apostila de Práticas. UFPE. 1999