O controle da queda de tensão em uma rede de distribuição deve ser precedido de análises preliminares, no que tange a especificidades operacionais do sistema. É necessário, inicialmente, verificar em quais das seguintes situações essa rede se encontra [1]:
- é trifásica simétrica, suprida por sistema trifásico com sequência de fase direta e com carga trifásica equilibrada entre os terminais de fase e o neutro;
- é trifásica simétrica, porém, a carga do trecho de rede, suprida entre os terminais de fase e o neutro é trifásica desequilibrada, ou, ainda, bifásica ou monofásica;
- é trifásica, assimétrica e a carga do trecho, suprida entre os terminais da fase e o neutro, é trifásica equilibrada ou desequilibrada ou, ainda, bifásica ou monofásica.
Para ilustrar a primeira situação, na Figura 1, é representado trecho de rede, em componentes de fase, através de suas impedâncias próprias e mútuas. Por simplicidade, foram omitidos os elementos em derivação, até mesmo porque, em redes de distribuição, eles não são significativos [2].

Tratando-se de rede trifásica simétrica, o trecho de rede é representável, em componentes simétricas, por seu circuito de sequência direta, conforme ilustração feita na Figura 2.

No caso geral a modelagem de qualquer trecho de rede pode ser feita por um circuito “pi” caracterizado por uma impedância série, interligando os seus terminais, e admitâncias nos terminais de entrada e de saída [2], conforme ilustrado na Figura 3.
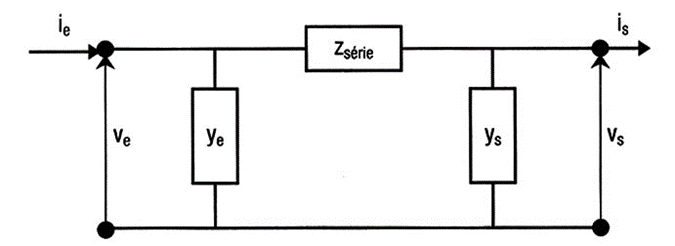
Para esse circuito, as tensões de entrada e saída podem ser relacionadas a partir das seguintes equações:
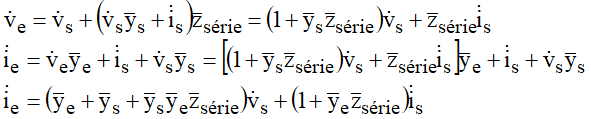
Para o caso de linha simétrica, as seguintes simplificações podem ser introduzidas:
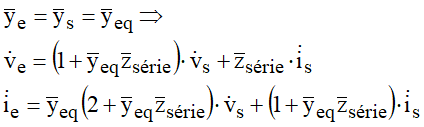
Por outro lado, em se tratando de linha curta, as admitâncias “shunt” podem ser desprezadas [2], levando a:

Atribuindo as coordenadas polares a cada uma das grandezas fasoriais:
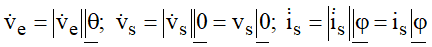
Observando que:

A equação anterior pode tomar a seguinte forma:
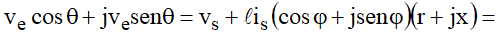
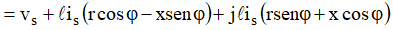
Tomando os módulos, vem:
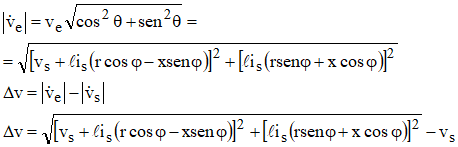
Observação importante:

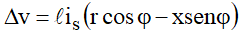
As seguintes considerações devem ser feitas [1]:
- no caso da carga ser modelada por corrente constante com a tensão a solução é direta (fornos a arco, lâmpadas fluorescentes, a vapor de mercúrio e a vapor de sódio são exemplos);
- caso a carga seja modelada por potência (motor de indução) ou impedância (capacitores ou aquecedores) constante com a tensão ocorrerá variação da corrente com o módulo da tensão e o procedimento de cálculo é iterativo.
O processo iterativo pode ser desenvolvido, seguindo-se os seguintes passos:

Na Figura 4 é apresentado script de rotina desenvolvida em Matlab [3] para simular as diversas situações descritas no processo iterativo citado.
| clear all close all clc % %Rotina para cáculo de queda de tensão em linha de distribuição % %clear all %close all % %Entrada dos dados % Vn=13.8; L=5; r=0.2053; x=0.3753; S=6; FP=0.92; tol=10^-5; disp(‘Escolha o código do modelo’) disp(‘1 – Corrente constante’) disp(‘2 – Potência constante’) disp(‘3 – Impedância constante’) q=input(‘Entre com o código do modelo: ‘); % %Cálculo dos valores por unidade (Vbase=13.8 kV e Sbase=100 MVA) % Vb=13.8; Sb=100; rpu=r*Sb/(Vb^2); xpu=x*Sb/(Vb^2); Spu=S/Sb; iFP=sin(acos(FP)); Vnpu=Vn/Vb; % %Modelo linha curta % %Queda de tensão – modelo de corrente constante % if q==1 ipu=Spu/Vnpu; dVpu=L*ipu*(rpu*FP+xpu*iFP); dVV=dVpu*Vb; Vs=Vn-dVV; fprintf(‘Tensão de entrada: %8.2f\n’,Vn/sqrt(3)); fprintf(‘Tensão de saida: %10.2f\n’,Vs/sqrt(3)); fprintf(‘Queda de tensão: %10.2f\n’,dVV/sqrt(3)); end % %Queda de tensão – modelo de potência constante % if q==2 dif=1; j=1; Vspu(1)=Vnpu; Nit(1)=1; while(dif>tol) j=j+1; Nit(j)=j; ipu=Spu/Vspu(j-1); dVpu=L*ipu*(rpu*FP+xpu*iFP); Vspu(j)=Vnpu-dVpu; dif=abs(Vspu(j)-Vspu(j-1)); end dVV=dVpu*Vb; Vs=Vn-dVV; fprintf(‘Numero de iterações: %4.0f\n’,j-1); fprintf(‘Tensão de entrada: %8.2f\n’,Vn/sqrt(3)); fprintf(‘Tensão de saida: %10.2f\n’,Vs/sqrt(3)); fprintf(‘Queda de tensão: %10.2f\n’,dVV/sqrt(3)); plot(Nit,Vspu) xlabel(‘Número das iterações’); ylabel(‘Tensão de saída, em pu’); grid on set(gca,’xtick’,Nit) end |
Observe que a rotina já incorpora exemplo específico, no qual a rede possui uma tensão de entrada de 13,8 kV, comprimento de 5 km, resistência série de 0,2053 OHM, reatância série de 0,3753 OHM e uma carga alimentada de 6 MVA de potência aparente, com fator de potência indutivo de 0,92. Verifique, também, que foi considerada, inicialmente, tolerância de 10-3 para a precisão nos resultados a serem obtidos. Ao rodar o programa, a tela de entrada, ilustrada na Figura 5, questiona qual o modelo para representação da carga.
| Escolha o código do modelo 1 – Corrente constante 2 – Potência constante 3 – Impedância constante Entre com o código do modelo: |
Escolhendo-se, por exemplo, o código 1, a saída será direta (sem iteração), com os resultados apresentados na Figura 6.
| Tensão de entrada: 7.97 Tensão de saída: 7.55 Queda de tensão: 0.42 |
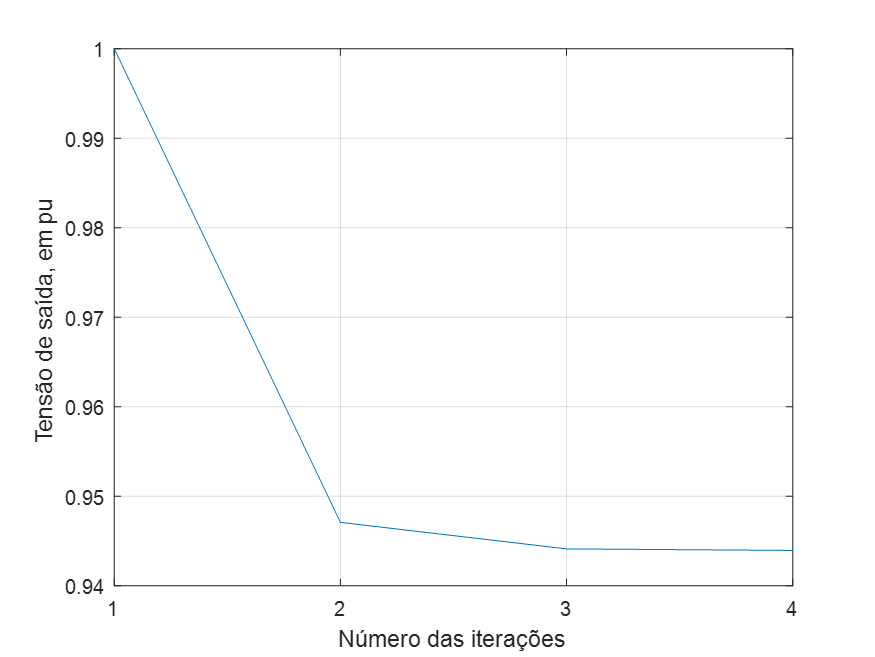
Caso a escolha for o código 2, a rotina registra quantas iterações foram necessárias para obtenção dos resultados apresentados na Figura 7. É construído, também, gráfico ilustrativo do processo iterativo empreendido para se chegar ao resultado, em consonância com a tolerância requerida (10-3), conforme registrado na Figura 8.
| Numero de iterações: 3 Tensão de entrada: 7.97 Tensão de saída: 7.52 Queda de tensão: 0.45 |
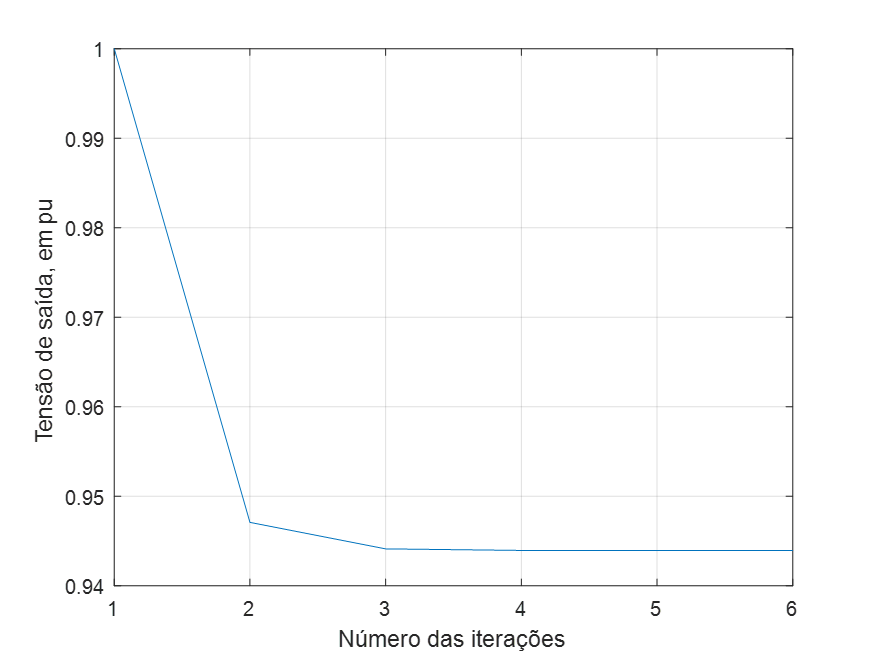
Caso fosse atribuída uma tolerância de 10-5, por exemplo, os resultados seriam os apresentados nas Figura 9 e 10, levando o processo iterativo a se prolongar, perseguindo a tolerância menor requerida. Registra-se que as diferenças numéricas só seriam observadas na quinta casa decimal.
| Numero de iterações: 5 Tensão de entrada: 7.97 Tensão de saida: 7.52 Queda de tensão: 0.45 |
TRECHO DE REDE TRIFÁSICA ASSIMÉTRICA COM CARGA DESEQUILIBRADA
Na Figura 11, é apresentada representação do trecho sob análise [1].
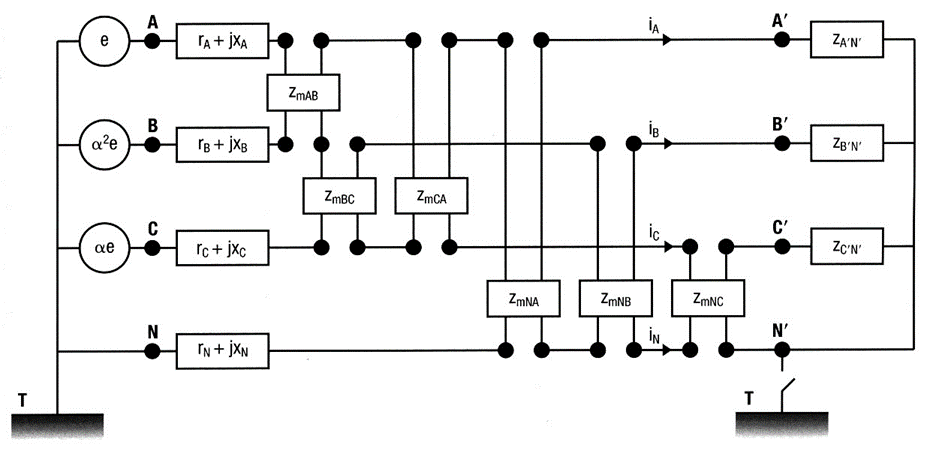
Em uma representação matricial poderiam ser escritas as seguintes relações:
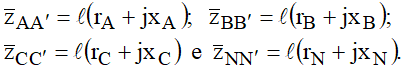
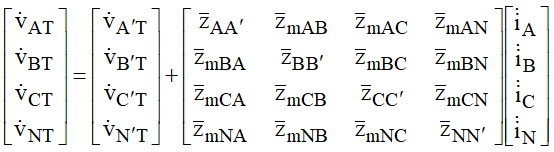
Fazendo:
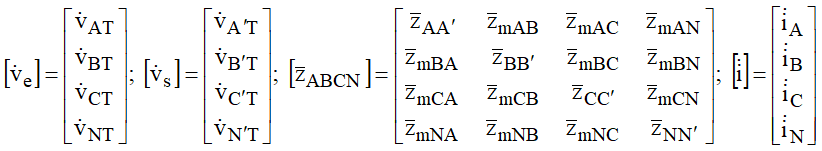
Resulta:
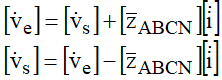
Do ponto de vista da carga, poderiam ser escritas as seguintes relações para as correntes:
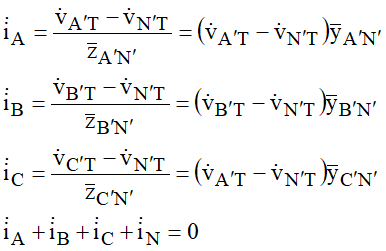
Em uma representação matricial resulta nas seguintes relações:
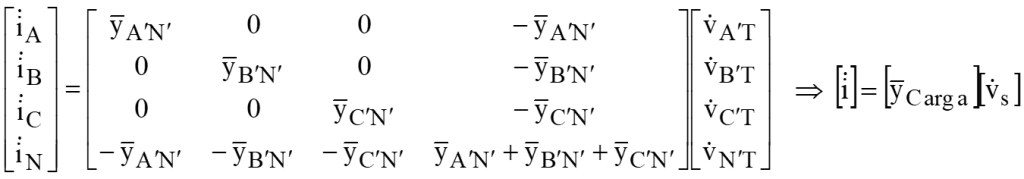
Substituindo na equação da tensão de entrada, vem:
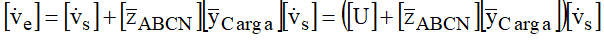
Para o caso de carga de impedância constante com a tensão a rede é calculada resolvendo-se as equações, levando a:
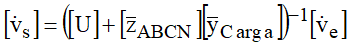
Em situações mais genéricas, em consonância com o tipo de carga alimentada, as seguintes considerações teriam que ser incorporadas:
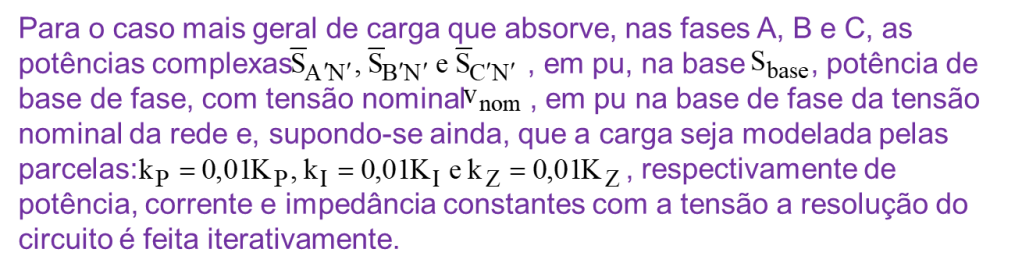


CONSIDERAÇÕES FINAIS
Neste post foram analisadas diversas situações em que a queda de tensão ao longo de uma rede de distribuição pode apresentar maior ou menor intensidade. Ênfase foi dada à característica da rede, que pode apresentar peculiaridades a depender do tipo de carga alimentada. Redes trifásicas equilibradas foram analisadas com maior profundidade, tendo-se apresentado e simulado modelo computacional específico para representar estudos de casos voltados para diversos tipos de carga. Foram feitos embasamentos para exercícios mais elaborados voltados para redes trifásicas desequilibradas, as quais podem ser foco de pesquisas especiais de estudantes de pós-graduação, procurando comparar eventuais rotinas computacionais que venham a ser elaboradas com enfoques/aplicativos clássicos constantes da literatura [4] – [6]. Há de se ressaltar que essas redes desequilibradas são frequentes, tendo em vista a heterogeneidade das cargas alimentadas, tornando a pesquisa proposta ainda mais significativa.
REFERÊNCIAS BIBLIOGRÁFICAS
- Kagan, N., Oliveira C. C.B., Robba E. J. “Introdução aos Sistemas de Distribuição de Energia Elétrica”. Editora Edgard Blucher. 2005.
- Fuchs, Rubens Dario, Transmissão de Energia Elétrica, Livros Técnicos e Científicos S. A. Editora EDUFU UNIVERSIDADE FEDERAL DE UBERLÂNDIA. 2015.
- MATLAB, “The Language of Technical Computing”, Massachusetts, United States, The MathWorks, 2010.
- ELGERD, O., I. Introdução à Teoria de Sistemas de Energia Elétrica. Editora McGraw-Hill, São Paulo, 1981.
- SANTOS, Liedson Oliveira dos. Ferramenta Computacional Para Determinação Do Fluxo De Potência Linearizado Em Sistemas Elétricos De Potência. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed. 03, Vol. 12, pp. 95-110. Março de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-eletrica/potencia-linearizado, DOI: 10.32749/nucleodoconhecimento.com.br/engenharia-eletrica/potencia-linearizado
- CEPEL. ANAREDE: Análise de sistemas elétricos de potência em regime permanente. https://www.cepel.br/produtos/anared-2/. Acessado em 08 de novembro de 2022.

Deixe um comentário