Cálculo e Medição de Parâmetros Elétricos de Linhas de Transmissão (Parte 1)

O transporte de energia é significativamente influenciado pelos valores dos parâmetros elétricos de suas linhas. A determinação desses parâmetros dentro de um mínimo rigor matemático é necessária. Seus valores dependem de sua configuração física e do meio no qual se encontram os condutores. Avaliações posteriores desses parâmetros através de medições têm sido perseguidas, com ênfase nos métodos que mantêm a linha em operação.

As imprecisões na caracterização desses parâmetros podem levar a diversas consequências para o sistema elétrico, quais sejam [1]:

• divergências nas medições operacionais;
• compensação de reativos além do necessário;
• extrapolação nos limites de segurança do sistema;
• alarmes indevidos nos sistemas de controle e supervisão;
• operação indevida da proteção.

METODOLOGIA DE CÁLCULO DOS PARÂMETROS ELÉTRICOS

São descritas a seguir as metodologias para cálculo dos parâmetros elétricos de uma linha aérea de transmissão em corrente alternada senoidal. Serão enfocados os cálculos da reatância indutiva, reatância capacitiva, resistência e condutância de dispersão. Nesta primeira parte, serão abordados os dois primeiros parâmetros e exemplo de aplicativos computacionais utilizados.

No que tange à reatância indutiva, considere um grupo de “n” condutores, a indutância seria obtida a partir de (1), considerando o efeito do solo [2].

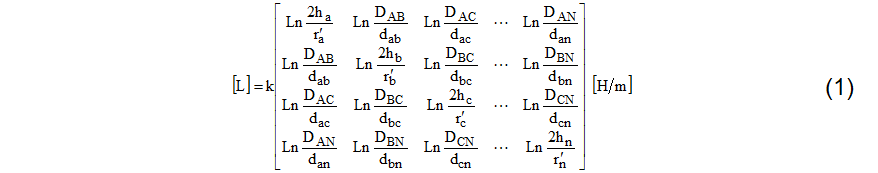
Onde:

• h_i – altura do condutor “i” em relação ao solo [m];
• d_ij – distância do condutor “i” ao condutor “j” [m];
• D_ij – distância do condutor “i” à imagem do condutor “j” [m];
• k – 2×10^-7;
• r’_i – raio de condutor fictício que não possui fluxo magnético interno, dado por:

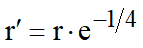
Matricialmente, a indutância seria obtida por: [L]=k[F], onde [F] é denominada “matriz dos coeficientes de campo”, onde:

A equação das reatâncias indutivas x_L em ohm/km seria dada por (2).

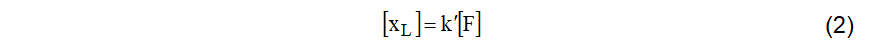
Onde k’ é dado por 12,5664 x f x 10^-4, sendo f a frequência do sistema em Hertz.

Algumas aproximações básicas são introduzidas nessa formulação [2]:

• condições normais de operação em linhas trifásicas em que as correntes no solo são insignificantes e o efeito sobre as indutâncias pode ser desprezado;
• o solo é considerado ideal (o que pode ser ajustado, como será visto);
• os condutores estão a alturas finitas e são paralelos ao solo, com altura h_i obtida em conformidade com a ilustração apresentada na Figura 1, onde H_i é a altura nominal da estrutura e f_i é a flecha no vão básico da linha de transmissão [3].

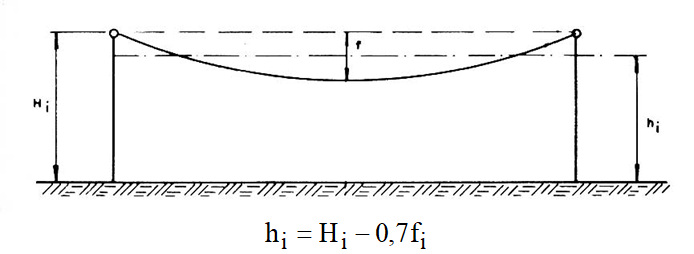
Outro conceito importante para o cálculo das reatâncias indutivas é o do raio médio geométrico dos condutores. Os cabos usados em linhas de transmissão e distribuição são construídos por encordoamento de um número variável de fios metálicos cilíndricos maciços, obtendo-se, dessa forma, condutores das mais variadas características mecânicas e composições, conforme ilustração feita na Figura 2 [3].

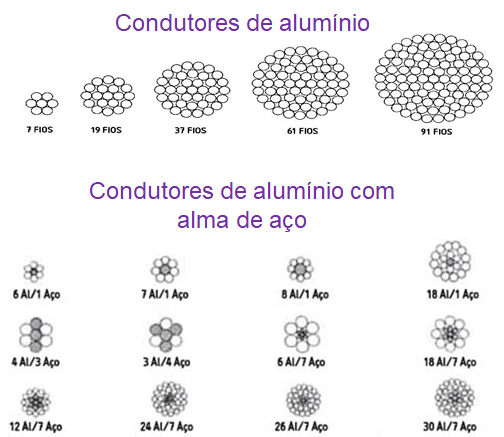
Os coeficientes de campo próprios devem refletir essas condições, a fim de que o fator encordoamento seja tomado em consideração nos cálculos elétricos.

Fazendo a simplificação de que haja uma distribuição uniforme da corrente por todos os filamentos, e considerando I_A=-I_B=I, vem [2]:

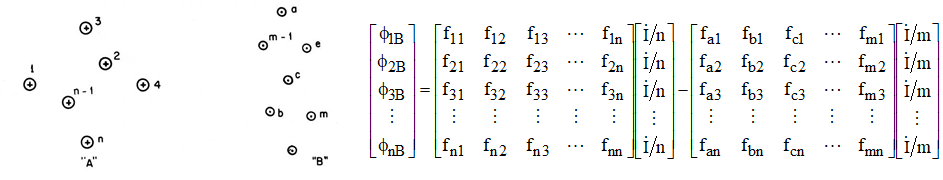
Pela definição de indutância:

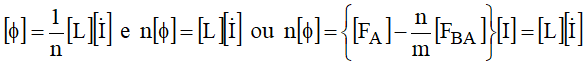
Logo:

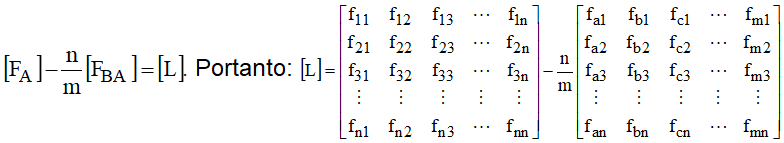
O valor médio da indutância por filamento seria dado por:

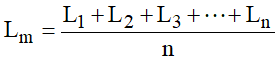
Como os filamentos estão em paralelo:

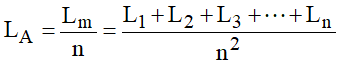
Introduzindo os valores de L₁, L₂, L₃, …, L_n após a substituição dos coeficientes de campo e a racionalização, vem: 

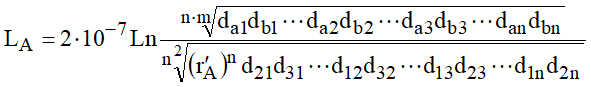
Nesta formulação, o numerador recebe o nome de distância média geométrica (DMG) entre os filamentos:

E o denominador recebe o nome de raio médio geométrico do condutor A:

De um modo geral, na prática, raramente será necessário determinar por cálculo os RMG dos cabos condutores. Dada a dificuldade de se considerarem, nos cálculos, todos os fatores modificativos, prefere-se lançar mão do RMG obtidos através de medição da indutância em um grande número de amostras de cabos de composições padronizadas. Seus valores médios são encontrados nas tabelas de características elétricas dos cabos condutores, publicadas pelos diversos fabricantes desse material, principalmente em se tratando de cabos não homogêneos.

Exemplificando para uma linha trifásica simples sem cabos para-raios, a equação de fluxos magnéticos seria dada por:

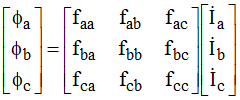
Para o sistema equilibrado:

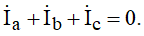
Considerando apenas o fluxo na fase a, seu valor será máximo no instante em que i_a=I_max. Nesse instante, nas fases b e c:

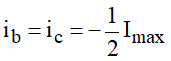
Aplicando o mesmo raciocínio para as fases b e c, vem:

Por outro lado, enfocando a linha alimentada por um gerador trifásico, na Figura 3 é ilustrada essa situação.

A partir das formulações dos fluxos por fase e da ilustração contida na Figura 2, as indutâncias aparentes seriam dadas por:

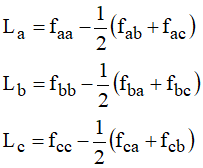
A partir desse conceito, na Figura 4 encontra-se ilustrado um trecho de linha, com as tensões e correntes trifásicas presentes, como também as indutância aparentes.

As quedas de tensão por fase seriam dadas por:

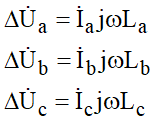
O sistema só se manterá equilibrado se L_a=L_b=L_c. Nessas condições:

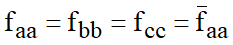
e:

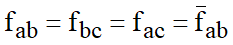
Dessa forma:

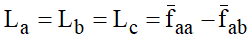
E, finalmente, chega-se a (3), onde L_s recebe o nome de indutância de serviço ou indutância de sequência positiva.

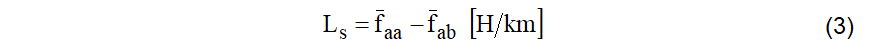
Enfocando um exemplo numérico, considere que uma linha de 13,8 kV foi construída com o padrão estrutural apresentado na Figura 5, com cabos CAA No 2 AWG. Determinar as reatâncias indutivas aparentes de cada fase e a reatância indutiva de serviço ou de sequência positiva.

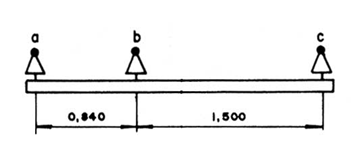
Desprezando inicialmente o efeito do solo, vem:

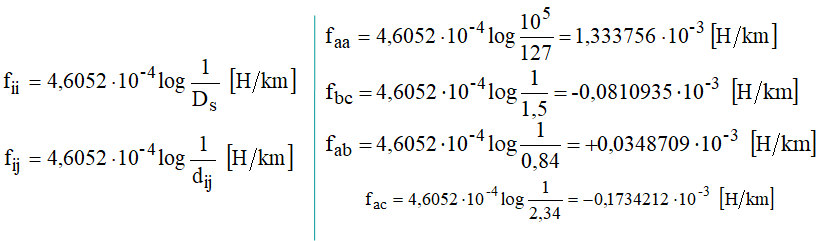
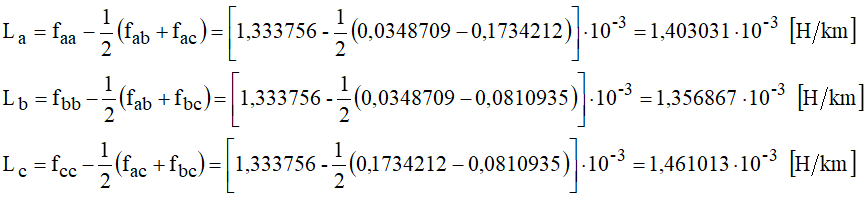
As reatâncias indutivas a 60 Hz, calculadas a partir dos valores acima, são:

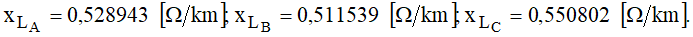
A reatância indutiva de sequência positiva é dada por:

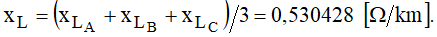
Essa reatância também poderia ser determinada pela expressão:

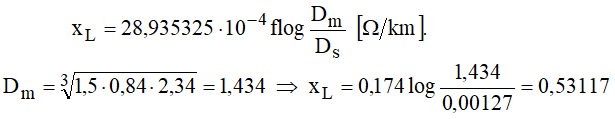
Considerando agora a presença do solo a uma altura média de 8 m sob a linha, neste caso, os coeficientes de campo se tornam:

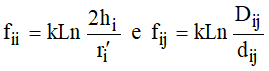
Neste caso, observando-se a Figura 5:

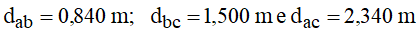
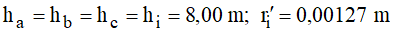
r’_i foi obtido em catálogo, para o cabo condutor informado.

As distâncias dos condutores às imagens dos condutores adjacentes podem ser obtidas em conformidade com a Figura 6, onde:

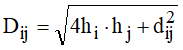
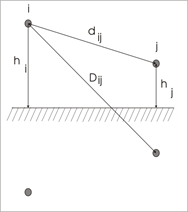
Levando a:

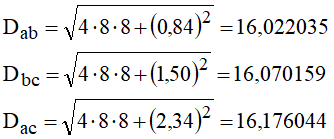
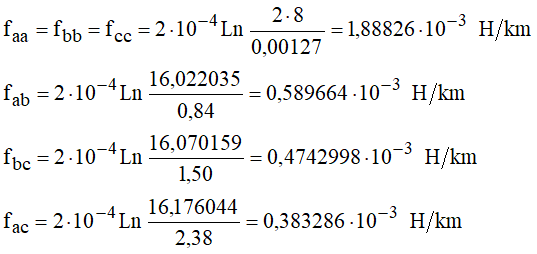
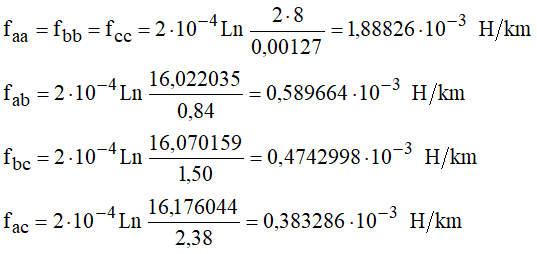
Obtendo-se as indutâncias aparentes:

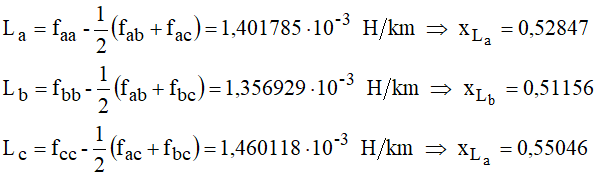
E as reatância indutiva de sequência positiva ou de serviço:

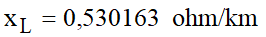
As Tabelas 1 e 2 resumem os valores obtidos.

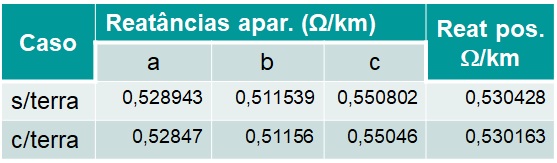
A partir das tabelas, as seguintes observações podem ser feitas:

• O efeito do solo é marcante nos valores dos coeficientes de campo;
• A maior diferença observada nos valores das reatâncias aparentes é de 0,08 %;
• A diferença entre os valores das reatâncias de sequência positiva é de aproximadamente 0,05%.

Home

Quanto à reatância capacitiva, vale lembrar os seguintes conceitos básicos:

• os condutores das linhas de distribuição energizados apresentam diferenças de potencial entre si e também com relação ao solo;
• essas diferenças indicam a presença de cargas elétricas distribuídas ao longo dos condutores;
• a linha se comporta como um capacitor de vários eletrodos, constituídos dos próprios condutores e o solo;
• quando da ligação da linha surge uma corrente chamada “corrente de carga”, a qual é quase insignificante para linhas curtas, mas pode atingir valores elevados para linhas longas.

Algumas relações fundamentais podem ser construídas a partir da Figura 7, na qual a carga elétrica de um condutor cilíndrico retilíneo, longo, isolado e suficientemente longe do solo e de outros condutores carregados, distribui-se uniformemente, formando ao seu redor um campo elétrico, homogêneo, cujas superfícies equipotenciais são também cilíndricas e concêntricas com o condutor.

O campo elétrico pode ser representado simbolicamente por linhas de fluxo elétrico, ou linhas de força, que emanam da superfície de um condutor de carga positiva e terminam em um outro condutor de carga negativa. O número de linhas de força é numericamente igual ao número de coulombs de sua carga elétrica.

Considerando uma superfície cilíndrica de raio x [m] concêntrica com o condutor, essa superfície é equipotencial. Sua área será, por metro linear de condutor, igual a 2px. A densidade de fluxo elétrico é dada por:

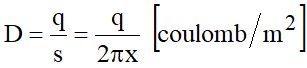
A intensidade de campo elétrico será:

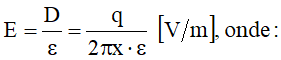
Nesse caso, em consonância com a Figura 8, a intensidade de campo elétrico E [V/m] em um ponto P situado nesse campo é numericamente igual à força em newton que atua sobre uma carga de um coulomb colocada nesse ponto.

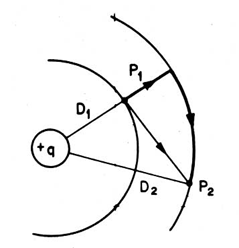
Para se deslocar uma carga de um coulomb de um ponto para um potencial mais alto realiza-se um trabalho, o qual é numericamente igual à diferença de potencial entre os pontos considerados.

Ainda em relação à Figura 8, considerando um condutor longo, retilíneo, possuindo uma carga positiva q [coulomb/m]. Os pontos P₁ e P₂ estão colocados, respectivamente, a distâncias D₁ e D₂ do centro do condutor. A carga positiva no condutor exercerá uma força de repulsão sobre uma carga positiva colocada no campo. Como D₂ é maior do que D₁, trabalho deve ser realizado para deslocar uma carga de P₂ para P₁, pois P₁ está a um potencial mais elevado do que P₂. A diferença de potencial é igual à quantidade de trabalho realizada por coulomb de carga deslocada. O valor instantâneo da diferença de potencial entre P₁ e P₂ será:

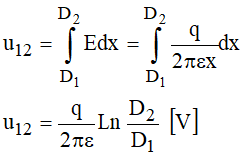
O valor da queda de tensão tanto poderá ser negativo como positivo, dependendo do sinal da carga q e do fato de se  considerar a queda de tensão desde um ponto próximo ao condutor energizado e um ponto mais remoto ou vice-versa.

No caso de dois condutores paralelos, com cargas +q e –q, possuindo os mesmos raios ra = rb = r, existirá entre os mesmos, à distância D/2, um plano XY de potencial nulo, conforme ilustração feita na Figura 9.

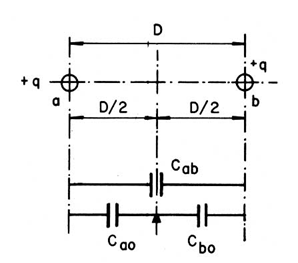
Definindo capacitância como carga por unidade de potencial, vem:

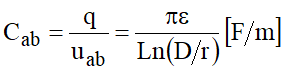
A capacitância entre os dois condutores a e b pode ser decomposta em duas capacitâncias parciais iguais: C_ao = C_bo = 2C_ab, para as quais se tem:

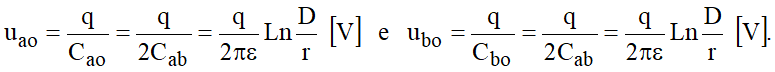
Por outro lado, ao se considerar um condutor carregado com uma carga +q a uma altura h do solo, conforme ilustração feita na Figura 10, à carga +q existente na superfície do condutor corresponde uma carga –q distribuída sobre a superfície do solo, onde terminam as linhas de fluxo que emanam da superfície do condutor A.

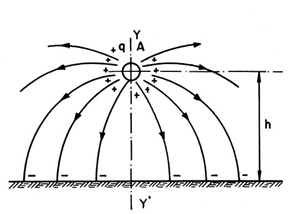
Nesta situação, é imaginado um condutor A’, o qual concentra toda a carga –q, compondo a forma do campo elétrico indicada na Figura 11.

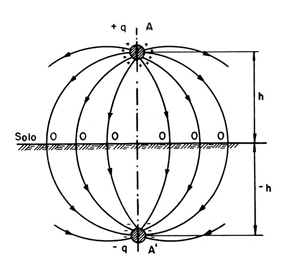
Para um sistema assim formado a diferença de potencial entre o condutor A e o solo é dada por:

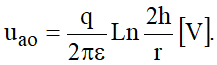
Considere agora dois condutores suspensos sobre o solo, conforme ilustração registrada na Figura 12.

O potencial do condutor a com relação ao solo será devido a sua carga própria, à carga de sua imagem e às cargas de b e b’:

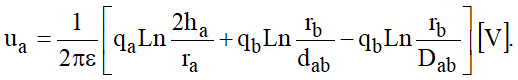
Ou:

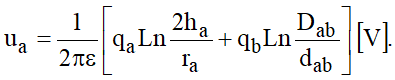
E:

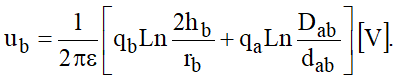
Matricialmente, pode ser escrito:

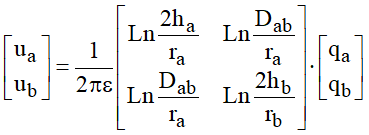
Nesta matriz, pode ser observado que: a matriz é simétrica em torno da diagonal; os termos da diagonal representam os potenciais devidos às cargas dos próprios condutores e de suas imagens, são os termos próprios; os termos fora da diagonal mostram a influência das cargas do condutor vizinho e de sua imagem sobre cada um dos condutores.

Em se tratando de uma linha de transmissão trifásica, as capacitâncias presentes são as ilustradas na Figura 13.

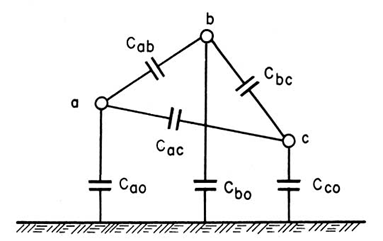
Neste caso a seguinte representação matricial pode ser construída:

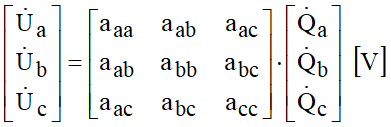
Onde cada termo a_ij representa os elementos logarítmicos construídos na relação matricial anterior. Explicitando o vetor de cargas, a seguinte relação matricial pode ser obtida:

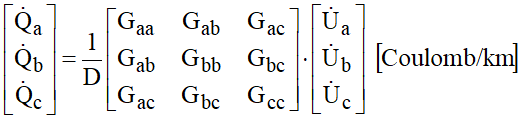
Onde D é o determinante da matriz anterior e G_ij os seus cofatores. Por outro lado, a partir da Figura 13 é possível construir a seguinte relação matricial:

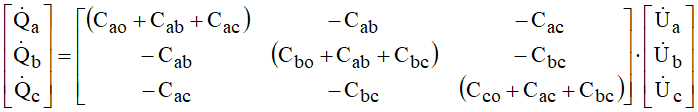
Seja a linha alimentada por um gerador trifásico, conforme ilustrado na Figura 14, se evidencia C_a, C_b e C_c como as capacitâncias equivalentes vistas do gerador.

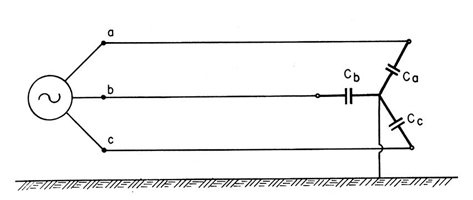
Nessas condições, pode-se escrever:

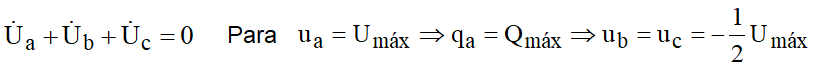
Pela equação matricial:

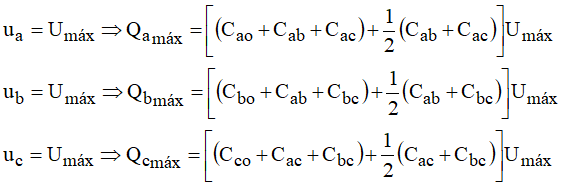
Essa última relação pode ser escrita como:

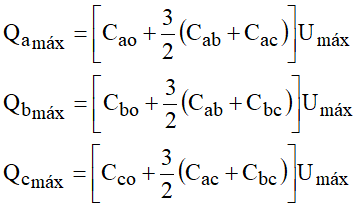
Lembrando que C=Q/U, vem:

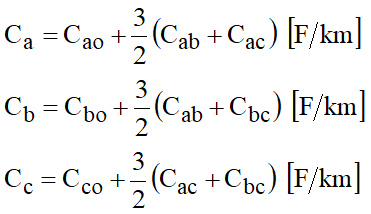
Essas são as capacitâncias equivalentes de uma linha trifásica. Elas põem em destaque o desequilíbrio eletrostático existente nas linhas. Para que ocorra o equilíbrio eletrostático entre as fases, a matriz [A] terá que ser uma matriz com termos iguais na diagonal e termos iguais fora da diagonal. Isso é obtido empregando-se transposições cíclicas na linha, conforme ilustrado na Figura 15.

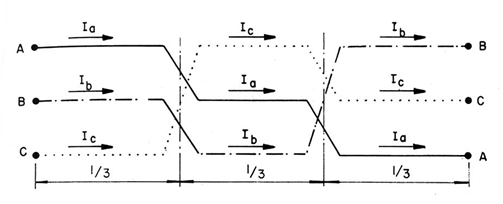
A equação matricial, considerando os três trechos de linha, se transforma em:

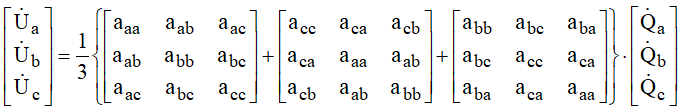
Operando a soma matricial, vem:

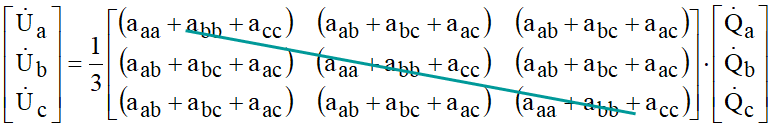
Essa última equação caracteriza o equilíbrio de fazes alcançado através das transposições. A matriz de coeficientes de potencial se torna:

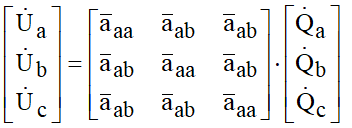
Efetuando a inversão da matriz anterior, vem:

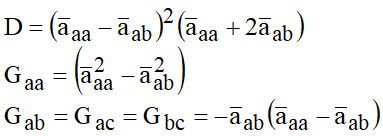
Os termos da matriz invertida serão:

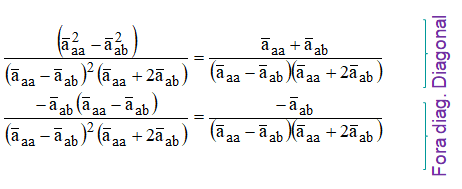
Substituindo esses valores nas capacitâncias:

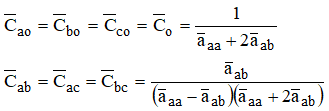
Se nas equações já construídas para C_a, C_b e C_c forem substituídos os valores médios, vem:

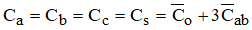
Obtendo-se finalmente a “capacitância de sequência positiva, ou de serviço (C_s):

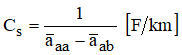
A reatância capacitiva, em derivação, de uma linha é definida por:

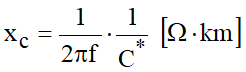
Para uma linha com L km, vem:

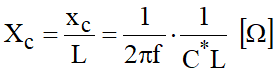
Sendo: f – frequência do sistema e C* [F/km] – capacitância unitária por condutor da linha ou condutor múltiplo; poderá ser qualquer das capacitâncias que foram definidas. Nos cálculos elétricos das  linhas, as capacitâncias de serviço são representadas como admitâncias, ou seja, na forma de susceptância de serviço: 

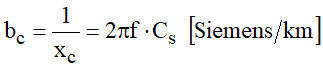
Para a linha inteira de comprimento L:

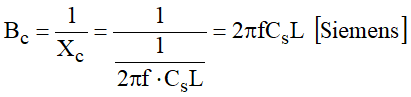
A título de exemplo, considere a linha de 13.8 kV, ilustrada na Figura 5. Determinar a capacitância de seqüência positiva, ou de serviço. Considerar que o plano de potencial nulo é o próprio solo e que os condutores estão a uma altura média de 8 m em relação ao mesmo. As seguintes equações seriam aplicáveis:

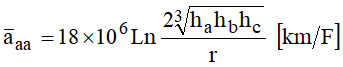
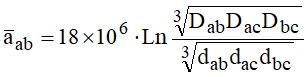
Observe que está sendo considerado desequilíbrio desprezível entre as fases. É como se a linha fosse transposta. Isso é razoável, considerando as pequenas extensões das linhas de distribuição. Operando, vem:

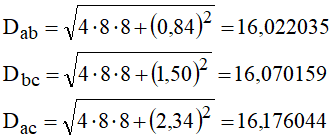
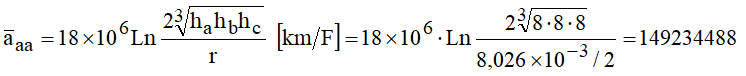
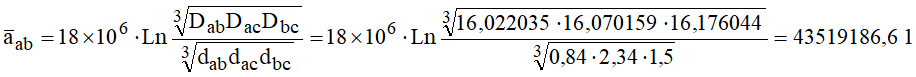
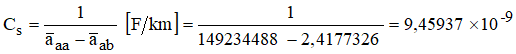
APLICATIVOS PARA CÁLCULO DE PARÂMETROS DE LINHA

Dentre os aplicativos disponíveis, serão abordados o Power_Lineparam do Matlab [4] e o LCC/ATP [5]. O Power_lineparam se destaca por:

• calcula as matrizes resistência, indutância e capacitância de um arranjo arbitrário de condutores de uma linha aérea de transmissão;
• para uma linha trifásica, as componentes simétricas também são calculadas.

Seja o exemplo ilustrado na Figura 16.

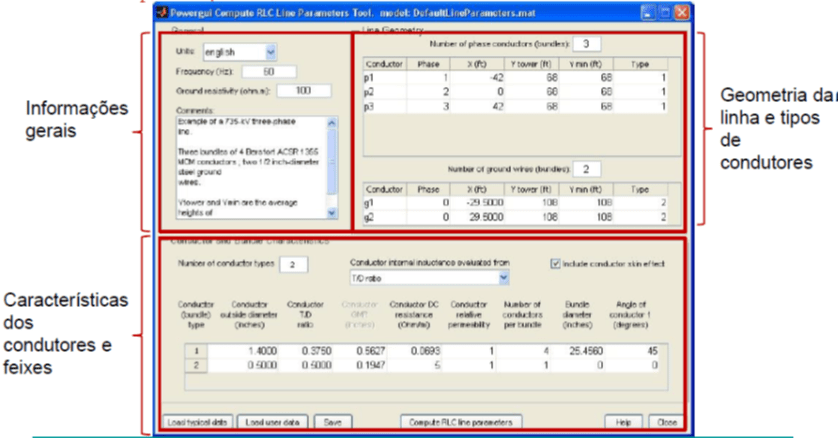
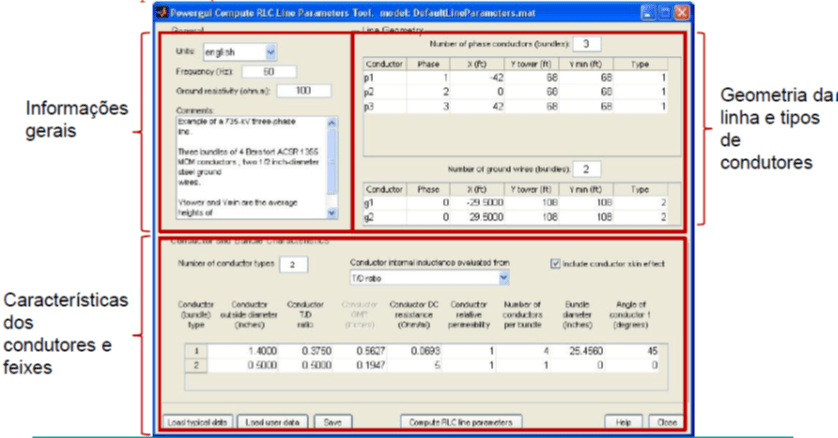
Quando se tecla o comando power_lineparam a tela GUI surge. No caso específico os dados da linha de circuito duplo estão preenchidos e apresentados na Figura 17.

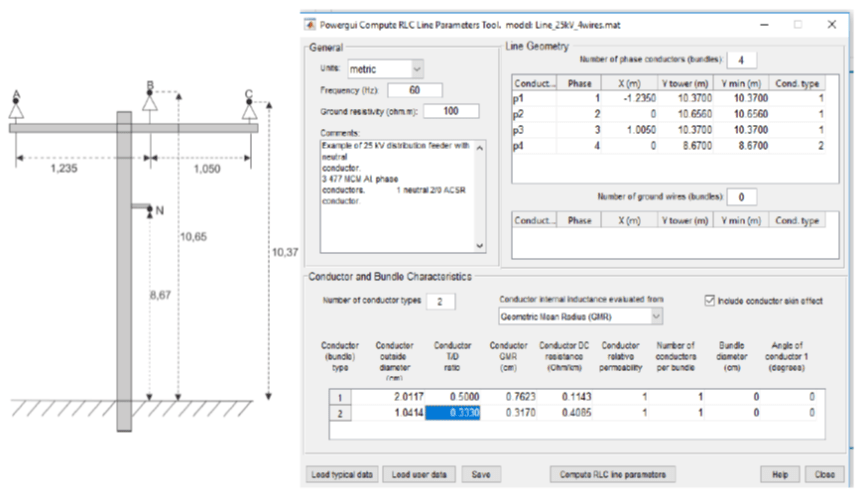
Para uma linha de circuito simples, considere o exemplo ilustrado na Figura 18.

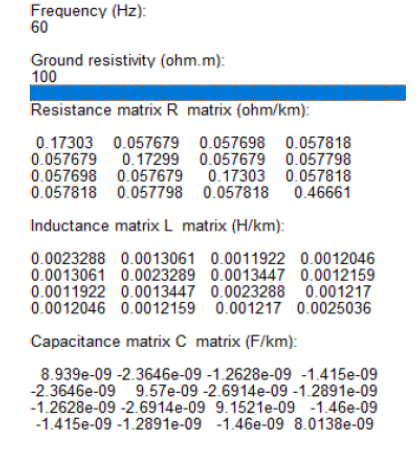
Para esse último caso, o aplicativo forneceria os seguintes resultados:

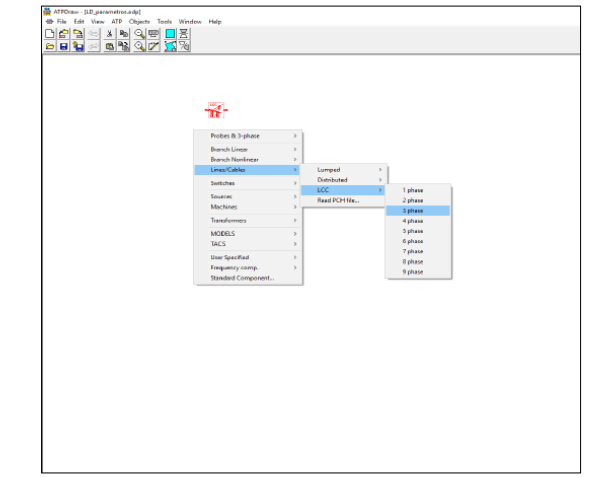
No caso do ACC/ATP, a função é acionada a partir do ATPDRAW ao clicar na tecla direita do mouse, surgindo a tela registrada na Figura 19.

Considerando o exemplo já ilustrado na Figura 5. A tela de entrada seria a registrada na Figura 20.

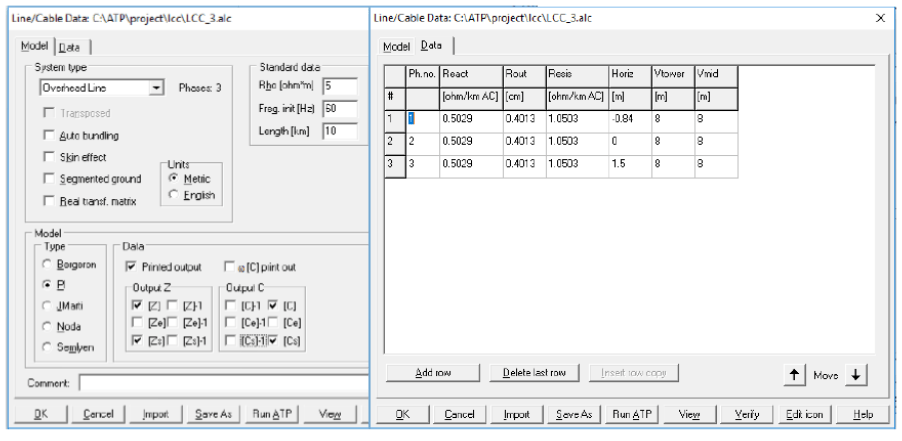
As saídas geradas pelo LCC/ATP encontram-se registras a seguir:

Home

CONSIDERAÇÕES FINAIS

Observa-se, portanto, que o cálculo dos parâmetros elétricos de uma linha aérea de transmissão trifásica incorpora complexidades além de meticulosos e exaustivos procedimentos. Neste contexto, o uso criterioso de aplicativos computacionais agregam ajudas substanciais.

No próximo post o tema será retomado, quando serão abordados os parâmetros resistência e condutância de dispersão, como também procedimentos para medição dos parâmetros elétricos de uma linha aérea de transmissão de energia elétrica..

REFERÊNCIAS BIBLIOGRÁFICAS

[1] Silva D. M., “Aplicação de Sincrofasores para Aferição de Parâmetros Elétricos de Linhas de Transmissão”. Dissertação de Mestrado. Universidade Federal de Pernambuco. 2008.

[2] Fuchs, R. D., “Transmissão de Energia Elétrica”. Livros Técnicos e Científicos S. A. Editora EDUFU, UNIVERSIDADE FEDERAL DE UBERLÂNDIA. 2015.

[3] Silva, A. A. P., “Modelagem para Repotencialização de Linhas de Transmissão Através da Aplicação de Condutores Especiais” Dissertação de Mestrado. Universidade Federal de Pernambuco. 2009.

[4] MATrix LABoratory (MATLAB), Version 14.1, Natick, MA, USA: The MathWorks, Inc., 2006.

[5] H. W. Dommel and S. Meyer, Eletromagnetic Transients Program (EMTP)/Alternative Transient Program (ATP). Version 2019. Bonneville Power Administration, Portland, OR, USA: BPA and Leuven EMTP Centre (LEC), 1960_2019.