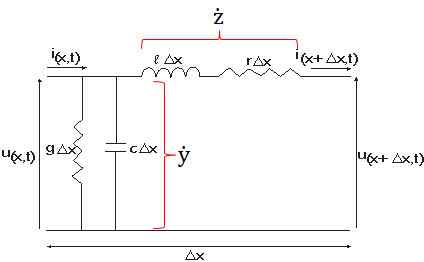
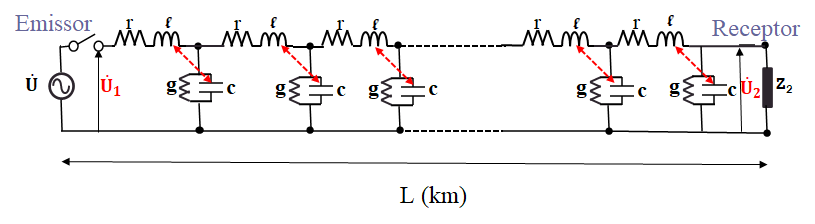
Dando sequência ao post anterior, o tema passará a ser enfocado, incorporando os elementos resistivos em série e condutivos em paralelo. Neste contexto, o segmento elementar (delta x) de uma linha de transmissão passará a ser representado, conforme circuito ilustrativo apresentado na Figura 1 [1].
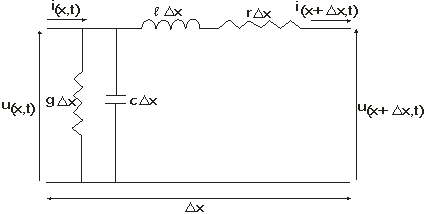
Neste contexto, a aplicação das leis de Kirchhoff ao circuito da Figura 1 levaria às equações diferenciais (1).
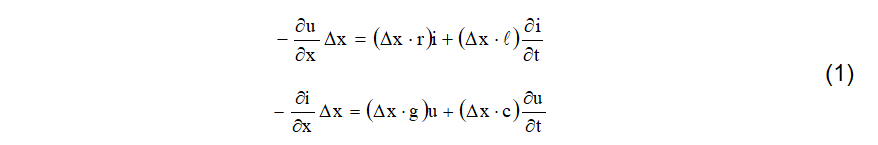
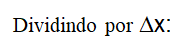
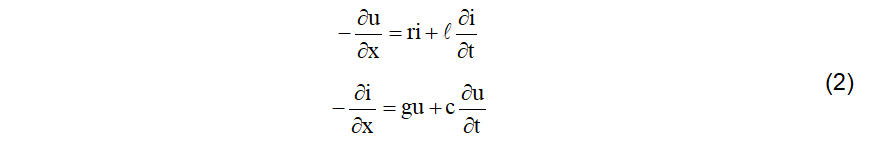
O sinal negativo significa que há uma queda de tensão e uma queda (fuga) de corrente. A equação (2), após diferenciações cruzadas e arrumações adequadas, se transformam em (3).
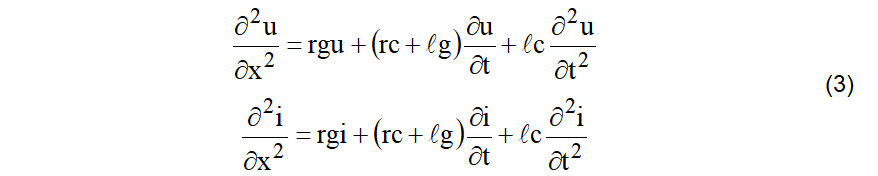
As equações (3) são chamadas “equações das ondas” ou “equações da telegrafia”. A solução dessas equações, em regime permanente, é obtida no domínio da frequência, fazendo-se as seguintes transformações:

Portanto, no domínio da frequência, as equações (3) se transformam em (4).
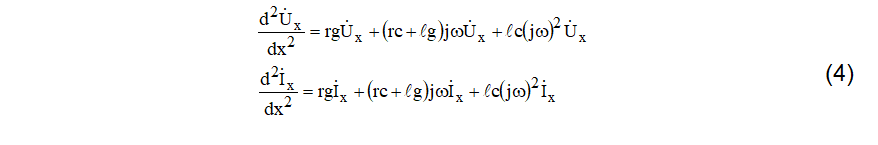
Arrumando as equações (4) elas tomam novas formas (5).
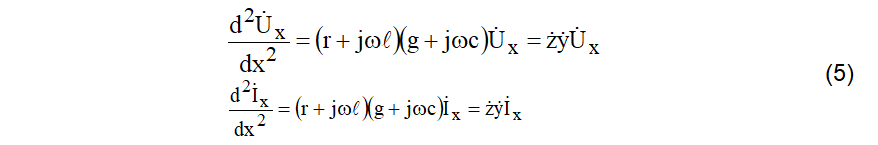
Onde:
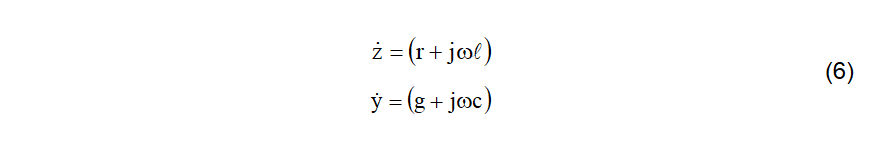
Observa-se que as equações (5) representam um sistema de equações diferenciais do segundo grau, no domínio da frequência. As soluções dessas equações são do tipo (7) [2].
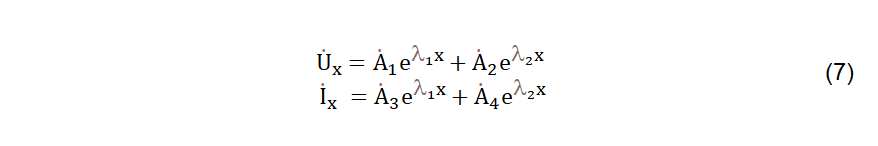
Os parâmetros “lambda” seriam obtidos a partir da substituição direta na equação (5), obtendo-se (8).
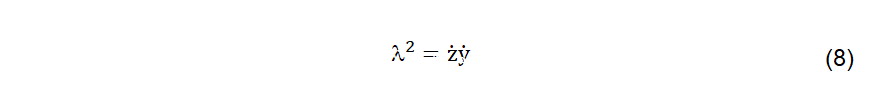
Cuja solução é dada por (9).
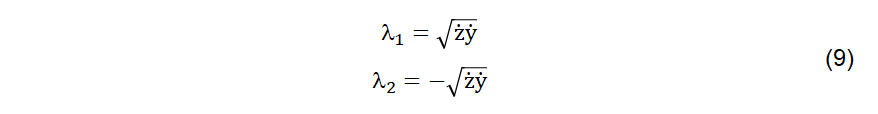
As constantes complexas “A” apresentadas na equação (7) podem ser obtidas, aplicando-se as condições de contorno, para x=0, no lado receptor da linha, implicando em (10).
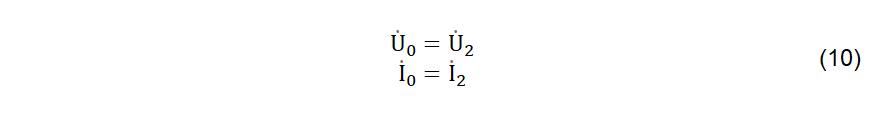
Por outro lado, as constantes “A” apresentadas em (7) possuem correlação entre elas, associadas a condições físicas vistas no post anterior: as tensões e correntes ao se deslocarem ao longo da linha estão correlacionadas da forma expressa em (11).
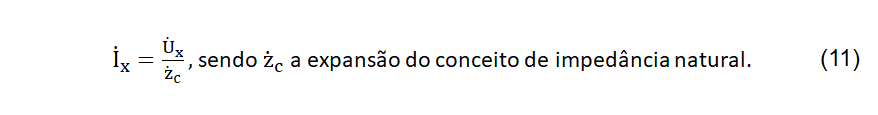
Esse novo conceito leva à definição da impedância característica da linha de transmissão, a qual pode ser expressa por (12), ressalvando-se que a impedância natural representa um caso particular, quando a linha não apresenta elementos resistivos e condutivos, ou seja, uma linha ideal.
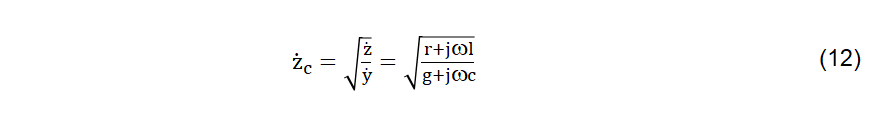
Os parâmetros r e g representam os elementos resistivos e condutivos, enquanto que l e c são, respectivamente, os elementos indutivos e capacitivos da linha linha de transmissão, por unidade de comprimento. As impedâncias e admitâncias por unidade de comprimento são obtidos desses parâmetros unitários e se encontram representadas na Figura 2.
Portanto, a aplicação de (9), (11) e (12) em (7) leva às equações (13).
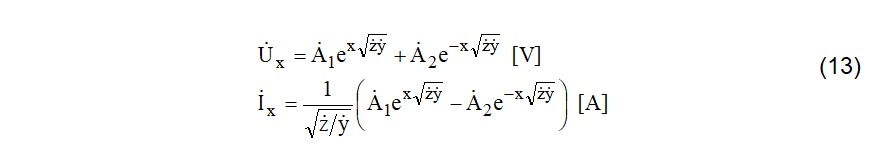
A aplicação das condições de contorno estabelecidas em (10) levam a (14).
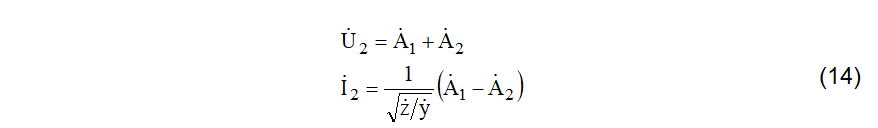
A resolução do sistema de duas equações e duas incógnitas expresso por (14) leva a (15).
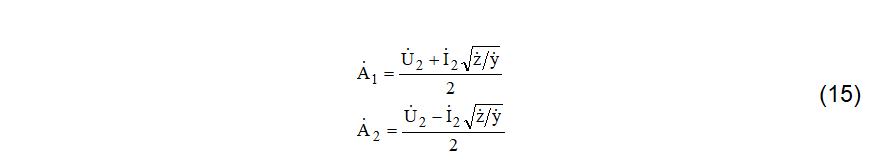
A substituição das constantes “A” encontradas em (15), nas equações (13), levam a (16).

Essas últimas equações são as chamadas “Equações Gerais das Linhas de Transmissão”. Elas permitem obter a tensão e a corrente em qualquer ponto “x” de uma linha de transmissão, conforme ilustração contida na Figura 3.

As grandezas tensão e corrente obtidas a partir de (16) são fasoriais, do tipo ilustrado em (17).

Para se obter os seus valores correspondentes, no domínio do tempo, a conversão ilustrada em (18), precisa ser realizada.
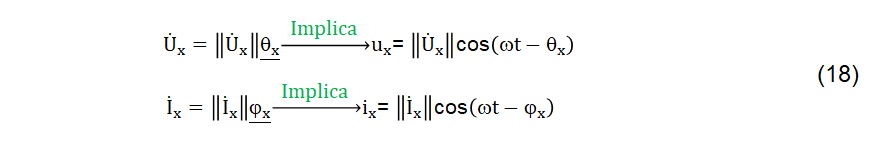
Por outro lado, vale considerar uma importante conceituação expressa em (19).

O termo exponencial das equações (16) podem ser escritos como (20).
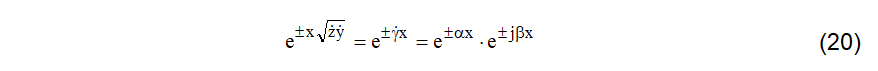
Portanto a função senoidal ao longo da linha sofre contínua alteração, expressa em (21).

Neste contexto, lembrando do conceito de impedância caraterística introduzido em (12), as equações (16) podem ser reescritas como (22).

Observando as equações (22), é possível distinguir as ondas viajantes de tensão e corrente no sentido positivo de “x” (ondas incidentes, termos com expoentes positivos) e no sentido negativo de “x” (ondas refletidas, termos com expoentes negativos). Uma outra observação é que essas equações retratam a solução do sistema de equações diferenciais, no estado permanente. Portanto, as ondas viajantes (incidentes e refletidas) permanecem na linha por tempo indeterminado, mesmo com a presença dos elementos resistivos e condutivos. Essas ondas são alimentadas constantemente pela fonte senoidal.

O CONCEITO DE COMPRIMENTO DE ONDA DE UMA LINHA
Quando a linha está operando em vazio ou em carga leve, a equação (22) para as tensões toma a forma (23).

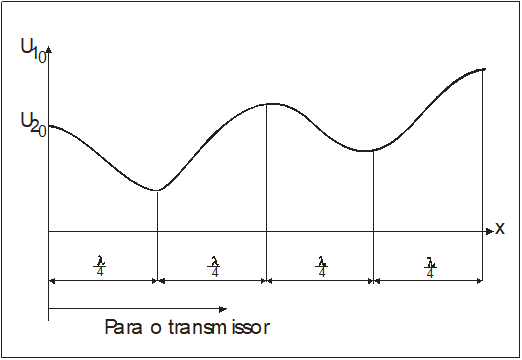
Portanto, a forma da tensão ao longo do comprimento da linha é também senoidal em “x”. Neste contexto, o comprimento de onda de uma linha de transmissão é definida como a distância entre dois pontos mais próximos da onda senoidal, cujas fases de oscilação estejam separadas de dois Pi [1], conforme se encontra ilustrado na Figura 4.
Pode ser mostrado que esse comprimento de onda é obtido por (24) [1].

A velocidade de propagação, como visto no post anterior, é obtida a partir de (25).

Observa-se que o conceito de comprimento de onda é meramente elétrico, pois depende da indutância e capacitância por unidade de comprimento e da frequência de operação do sistema.
Considerando a velocidade de propagação da onda viajante igual aproximadamente a velocidade de propagação da luz no vácuo (3×108 [m/s]), para sistemas operando a 50 ou a 60 Hz, os comprimentos das ondas seriam 6.000 e 5.000 km, respectivamente. Portanto, uma linha pode ter o comprimento físico de 2 km, mas o seu comprimento de onda ser de 5.000 km, uma vez que só depende dos seus parâmetros elétricos.
Algumas verificações importantes podem ser feitas a partir da Figura 4:
- uma linha com o comprimento físico igual ou próximo a um quarto do comprimento de onda certamente apresentaria um comportamento operacional péssimo, pois, em vazio ou em carga leve, a tensão no lado receptor seria bem superior à tensão no lado emissor;
- por outro lado, uma linha cujo comprimento físico seja igual ou próximo de meio comprimento de onda apresentaria condições operacionais excelentes, pois em vazio ou em carga leve, as tensões nos terminais emissor e receptor seriam praticamente iguais e as tensões ao longo da linha seriam bem inferiores, diminuindo as questões relacionadas com as perdas por efeito corona.
OPERAÇÃO DA LINHA NA POTÊNCIA NATURAL/CARACTERÍSTICA
Quando a linha opera em sua potência natural/característica significa que a carga alimentada no terminal receptor possui impedância igual à impedância natural/característica da linha. Nessas condições, as relações registradas em (26) podem ser aplicadas.
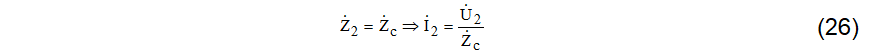
Substituindo (26) nas equações da linha, (22), resulta em (27).
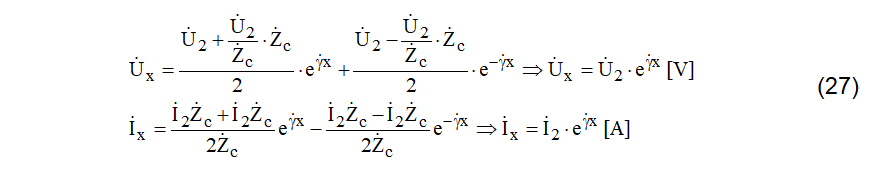
Nestas últimas equações observam-se que desaparecem os segundos termos das equações, os quais estão associados às ondas refletidas de tensão e corrente. Uma outra constatação se extrai, quando se divide a equação resultante para a tensão pela equação resultante para a corrente, levando a (28).

Portanto, o defasamento entre tensão e corrente só depende do fator de potência da carga. A linha se comporta como um circuito puramente resistivo (série/paralelo), ou seja, ela não precisa de energia reativa externa para manutenção dos seus campos elétricos e magnéticos. A única energia absorvida pela linha é a energia ativa destinada a cobrir as perdas por efeito Joule e corona/dispersão. As energias reativas necessárias são extraídas alternadamente dos campos magnéticos e elétricos da própria linha, conforme ilustra a Figura 5. Não é necessário, portanto, que a fonte forneça essa energia reativa. Tal condição retrata um ponto operacional ótimo em que as perdas na linha se tornam mínimas.
Nesta condição operacional, a potência fornecida no terminal receptor será dada por (29).
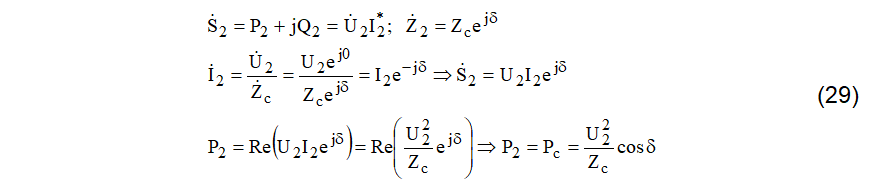
Pc é denominada “potência característica”. Como em geral o argumento da impedância característica é muito pequeno, entre 1 e 5o, valem as expressões (30).
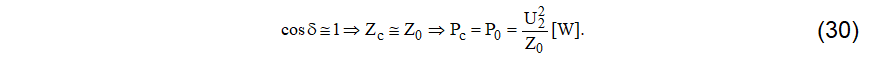
Para um sistema trifásico pode se escrever (31).
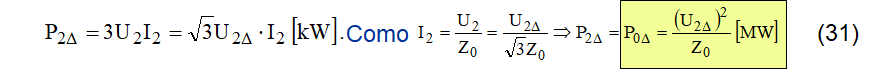
Esta última equação é denominada “potência natural da linha trifásica”. Ela permite, em primeira instância, identificar a classe de tensão desejável para uma linha de transmissão, caracterizando que a sua potência natural será igual à potência da carga a ser alimentada. A Tabela 1 ilustra essa condição, para diferentes padrões estruturais básicos e configurações diversas dos feixes de condutores por fase. Os valores não preenchidos indicam condições não usuais, quer do ponto de vista econômico, quer do ponto de vista técnico-operacional, diante das elevadas perdas por efeito corona para classes superiores a 500 kV.

É neste contexto que surge o conceito de linha de potência natural/característica elevada. Este conceito enfoca a necessidade de se minimizar a relação indutância / capacitância por unidade de comprimento. Essa relação é minimizada pela escolha otimizada do padrão estrutural da linha e da geometria dos feixes de condutores. Algumas restrições devem ser observadas nesta busca, além das questões econômicas envolvidas, quais sejam:
- distâncias condutor-solo;
- corona crítico visual;
- gradiente eletrostático ao nível do solo;
- efeitos eletromagnéticos;
- esforços mecânicos envolvidos.
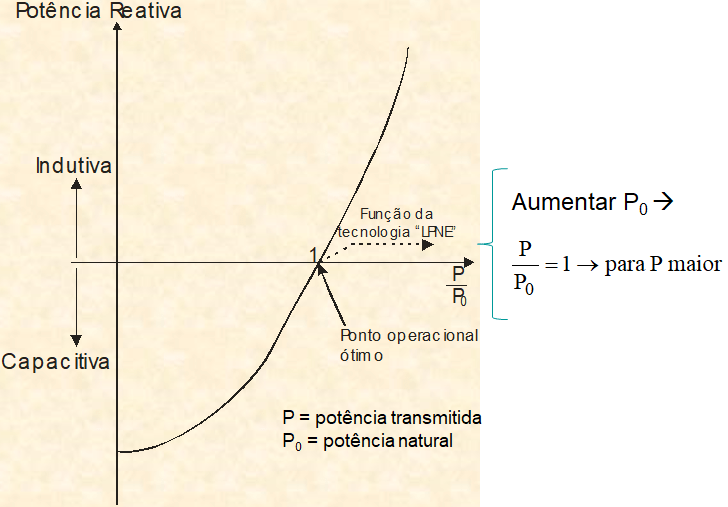
Na Figura 6 é ilustrada a condição operacional de uma linha (capacitiva ou indutiva), em função da relação potência transmitida/potência natural (P/P0). É observado que, em carga leve a linha é muito capacitiva, ou seja absorve muita energia capacitiva da fonte para alimentar o seu campo elétrico. Com o crescimento da carga, a linha vai se tornando menos capacitiva até chegar a condição P/Po = 1. Nesta condição, a linha está operando em sua potência natural e não existe a necessidade de absorver energia reativa para alimentação dos seus campos (eles se auto alimentarão). Essa é aquela condição em que as perdas na linha são mínimas. A tecnologia LPNE busca aumentar a potência natural e caracterizar uma condição operacional (P/P0 = 1) para uma potência alimentada ainda maior. A partir deste ponto, como indica a figura, a linha se torna indutiva, ou seja, passa a absorver energia reativa indutiva da fonte para alimentar o seu campo magnético.
CONTEXTUALIZAÇÃO TECNOLÓGICA
O conceito de onda viajante remete à transmissão em longas distâncias. No Brasil, a tecnologia foi bastante analisada para transmissão da energia gerada na Região Norte do país (Usina de Belo Monte) para o Sudeste, perfazendo mais de 2.000 km de linha [3]. Infelizmente a opção foi feita pela tecnologia em corrente contínua (CC). A transmissão em corrente alternada (AC), em meia onda, teria sido uma excelente oportunidade para o Brasil desenvolver tecnologia própria, podendo vir a se tornar referência mundial, diferentemente da opção CC, na qual o país permanece dependente tecnologicamente. Um outro grande argumento favorável à tecnologia AC é que, ao longo da linha se poderia agregar novas subestações, propiciando o desenvolvimento das regiões atravessadas.
Diversas tecnologias vêm sendo desenvolvidas para recapacitar linhas em operação, levando-a a estágios superiores de potência natural, com todas as vantagens inerentes já comentadas. As tecnologias levam a inserção de condutores, suspensos aos originais (super festão) [4] [5], ou formando uma nova geometria de feixes de condutores [6]-[7].

CONSIDERAÇÕES FINAIS
A energização de uma linha de transmissão AC é um processo relativamente complexo, o qual exige cuidados especiais, tanto nas condições transitórias, quanto em estado permanente. Nas condições transitórias o terminal receptor pode ser submetido a sobretensões duas vezes a tensão inserida no lado emissor. Já no estado permanente, a linha é submetida a ondas viajantes de tensão e corrente, que devem ser devidamente consideradas. Cuidados especiais devem ser buscados no intuito de assegurar patamares aceitáveis de tensão, quer em seus terminais, quer ao longo da linha. Tais situações remetem à necessidade de aplicação de equipamentos externos que assegurem a compensação operacional adequada. Tais temas serão objeto de novos posts.
REFERÊNCIAS BIBLIOGRÁFICAS
[1] Fuchs R. D., Transmissão de Energia Elétrica, Livros Técnicos e Científicos S. A. Editora EDUFU – UNIVERSIDADE FEDERAL DE UBERLÂNDIA. 2015.
[2] Sterwart J., Cálculo Vol. II, ebook AMAZON. 2017.
[3] Fernandes J. H. M., et al., Eletronorte and the challenge of long-distance transmission in Brazil. Beinal CIGRE. 2008.
[4] Quijada J. E. M. Recapacitação de Linhas Aéreas de Transmissão de Energia Elétrica Através da Incorporação de Condutor Adicional em Subvãos. Dissertação de Mestrado. UFPE. 2019.
[5] Regis O. Jr., Dart F. C., CRUZ A. L. P, Avaliação Comparativa Das Concepções de Linhas de Potência Natural Elevada em 500 kV Utilizadas no Brasil. XIII ERIAC. CIGRE, Puerto Iguazú – Argentina, 2009.
[6] Pessoa Neto, A. et al., Novos Métodos Para Aumento de Potência de LT até 230kV: Estudos, Projeto e Implantação Comercial. SNPTEE, Foz do Iguaçu – Paraná – Brasil, 1999.
[7] Jamnani, D. J., Patel, V., Surge Impedance Loading Level Enhancement of 765 kV Long EHV AC line Through Bundle Configurations. Biennial lnternational Conference on Power and Energy Systems: Towards Sustainable Energy (PESTSE). IEEEE, 2016.
[8] Santos A. A. F., et al., Aplicação de Técnicas de LPNE em Linhas de Distribuição. Eletricidade Moderna. Julho de 2007.

Deixe um comentário